Lab Manual: Determination of Capacitance by Leakage Method

DETERMINATION OF CAPACITANCE BY LEAKAGE METHOD

1. AIM

To determine the capacitance of a given Capacitor using the leakage method.

2. APPARATUS USED

  • Capacitor of unknown capacitance
  • High resistance voltmeter (electrostatic voltmeter)
  • Battery or DC power supply (100V)
  • Charging key (K₁)
  • Discharging key (K₂)
  • Stop watch or timer with seconds precision
  • Connecting wires
  • Insulating stand for the capacitor

3. DIAGRAM

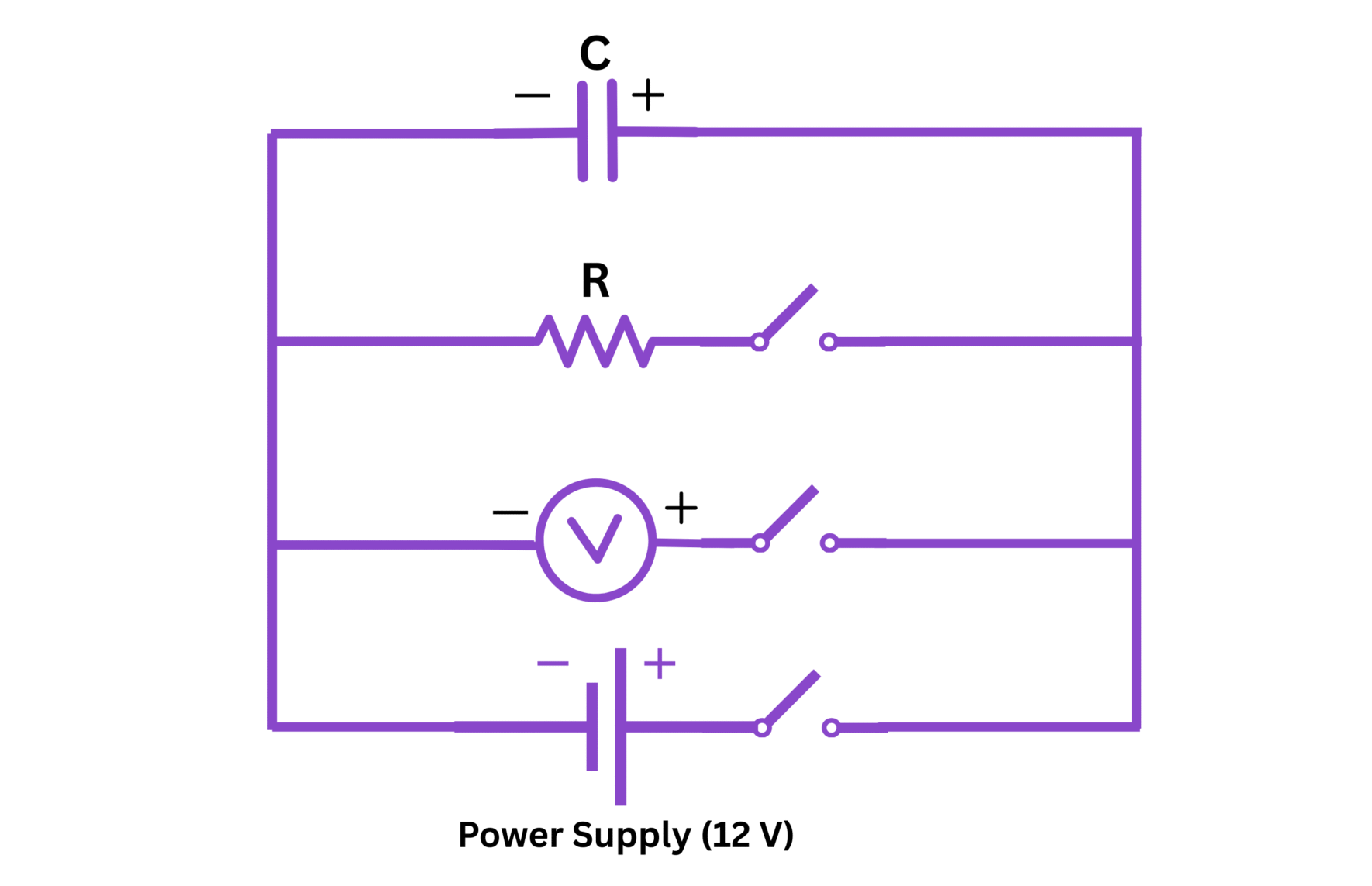
capacitance of capacitor by leakage method

Fig. 1: Circuit diagram for the determination of capacitance using leakage method

4. THEORY

The leakage method for determining capacitance is based on the principle that when a charged capacitor is left isolated, it gradually loses its charge due to the leakage through the dielectric or across the surface of the capacitor. This leakage current can be modeled as a high-value resistor connected in parallel with the capacitor.

When a capacitor is charged to a potential difference V₀ and then left isolated, the voltage across its terminals decays exponentially with time according to the equation:

$$V = V_0 e^{-\frac{t}{RC}}$$

Where:

  • V is the voltage across the capacitor at time t
  • V₀ is the initial voltage to which the capacitor was charged
  • R is the equivalent leakage resistance
  • C is the capacitance of the capacitor
  • t is the time elapsed since the capacitor was isolated

Taking the natural logarithm of both sides:

$$\ln\left(\frac{V}{V_0}\right) = -\frac{t}{RC}$$

This equation represents a straight line when ln(V/V₀) is plotted against t, with a slope of -1/RC. By measuring the voltage across the capacitor at different times and plotting the natural logarithm of the voltage ratio against time, we can determine the time constant RC of the circuit. If the leakage resistance R is known, the capacitance C can be calculated.

In practice, if the leakage resistance is very high (which is often the case for good capacitors), we can use an approximation. For small discharge times compared to the time constant RC:

$$C = \frac{(V_0 - V)t}{RV_0}$$

5. FORMULA

From the theory, the capacitance can be determined using the following formula:

$$C = \frac{-t}{R \ln\left(\frac{V}{V_0}\right)}$$

Where:

  • C is the capacitance in farads (F)
  • R is the leakage resistance in ohms (Ω)
  • V₀ is the initial voltage in volts (V)
  • V is the voltage after time t in volts (V)
  • t is the time in seconds (s)

If we observe voltage readings at equal time intervals, we can also use:

$$C = \frac{0.4343 \times t}{R \times \log_{10}\left(\frac{V_1}{V_2}\right)}$$

Where V₁ and V₂ are voltages at two different times separated by time interval t.

6. PROCEDURE

  1. Set up the circuit as shown in the diagram. The capacitor is initially uncharged.
  2. Close key K₁ while keeping key K₂ open. This will charge the capacitor to the battery voltage V₀.
  3. Note the initial reading V₀ on the voltmeter.
  4. Open key K₁ to isolate the charged capacitor (leaving K₂ open).
  5. Start the stopwatch immediately after opening K₁.
  6. Record the voltage across the capacitor at regular time intervals (e.g., every 30 seconds) for about 10 minutes or until the voltage has decreased significantly.
  7. After completing the readings, close key K₂ to discharge the capacitor completely.
  8. Repeat the experiment at least three times for consistency.
  9. Calculate the natural logarithm of the ratio V/V₀ for each time reading.
  10. Plot a graph of ln(V/V₀) against time t.
  11. Determine the slope of the graph, which equals -1/RC.
  12. Calculate the capacitance using the known value of the leakage resistance R.

7. OBSERVATION TABLE

Initial voltage V₀ = ________ volts

Leakage resistance R = ________ ohms

S.No. Time t (seconds) Voltage V (volts) V/V₀ ln(V/V₀)
1 0 V₀ = 1.000 0.000
2
3
4
5
6
7
8

8. CALCULATIONS

From the graph of ln(V/V₀) against time t:

Slope of the graph = ________

The slope is equal to -1/RC, therefore:

$$-\frac{1}{RC} = \text{Slope}$$

$$C = \frac{-1}{R \times \text{Slope}}$$

Substituting the values:

$$C = \frac{-1}{(\_\_\_\_\_\_\_ \Omega) \times (\_\_\_\_\_\_\_)}$$

$$C = \_\_\_\_\_\_\_ \text{ farads}$$

Convert the result to appropriate units (μF or pF):

$$C = \_\_\_\_\_\_\_ \mu\text{F}$$

9. RESULT

The capacitance of the given capacitor determined by the leakage method is ________ μF.

The percentage error in the measurement can be calculated as:

$$\text{Percentage Error} = \frac{|\text{Measured Value} - \text{True Value}|}{\text{True Value}} \times 100\%$$

If the true value is known: Percentage Error = ________%

10. PRECAUTIONS

  1. Ensure that the capacitor is completely discharged before starting the experiment.
  2. The voltmeter used should have a very high input impedance to minimize its loading effect on the circuit.
  3. Avoid touching the capacitor terminals during the experiment to prevent additional leakage paths.
  4. Keep the capacitor and circuit components on an insulating stand to minimize leakage to ground.
  5. Ensure good insulation in all connections and minimize contact resistance.
  6. The environment should be dry to prevent humidity-related leakage effects.
  7. Temperature should be kept constant throughout the experiment, as temperature variations can affect leakage resistance.
  8. Take readings at regular intervals and be precise with the timing.
  9. When dealing with high voltages, ensure proper safety measures are followed.
  10. Repeat the experiment multiple times for more accurate results.

11. VIVA VOICE QUESTIONS

1. What is capacitance and what is its SI unit?
Capacitance is the ability of a body to store electrical charge. It is defined as the ratio of the charge stored to the potential difference applied. The SI unit of capacitance is the farad (F), though in practice, microfarads (μF) or picofarads (pF) are commonly used.
2. Why is the leakage method suitable for measuring large capacitances?
The leakage method is suitable for measuring large capacitances because it uses the natural discharge characteristic of the capacitor through its own leakage resistance. For large capacitances, this discharge happens slowly enough to be measured accurately with standard equipment. Additionally, the method doesn't require AC sources or high-frequency measurements that might be affected by parasitic effects in large capacitors.
3. What factors affect the leakage resistance of a capacitor?
Factors affecting leakage resistance include: the type and quality of dielectric material, temperature (higher temperatures generally decrease leakage resistance), humidity and environmental conditions, applied voltage (higher voltages may cause increased leakage), age and degradation of the capacitor, and surface contamination on the capacitor body.
4. Why must the voltmeter used have a very high resistance?
The voltmeter must have a very high resistance to prevent it from providing an additional discharge path for the capacitor. If the voltmeter resistance is comparable to the leakage resistance of the capacitor, it will cause the capacitor to discharge faster than it would through its own leakage resistance alone, leading to inaccurate measurements of the capacitance.
5. How does temperature affect the capacitance measurement using this method?
Temperature affects the leakage resistance of the capacitor, which is a critical parameter in this method. Higher temperatures generally reduce the leakage resistance, leading to faster discharge and potentially different measured capacitance values. Temperature also affects the dielectric properties of the capacitor, which might slightly change its actual capacitance.
6. What are the limitations of the leakage method?
Limitations include: it's time-consuming for good quality capacitors with high leakage resistance; accurate knowledge of the leakage resistance is required; environmental factors like temperature and humidity can affect results; the method is less accurate for small capacitances; and it assumes the leakage resistance remains constant throughout the measurement, which may not always be true.
7. How does the capacitance of a parallel plate capacitor depend on its physical dimensions?
For a parallel plate capacitor, the capacitance C is given by C = ε₀εᵣA/d, where ε₀ is the permittivity of free space, εᵣ is the relative permittivity (dielectric constant) of the material between the plates, A is the area of overlap between the plates, and d is the distance between the plates. So capacitance increases with larger plate area and smaller plate separation.
8. Why does the voltage across the capacitor decrease exponentially with time during discharge?
The voltage decreases exponentially because the discharge rate is proportional to the voltage itself. As the voltage decreases, the current through the leakage resistance also decreases, which slows down the rate of discharge. This relationship leads to an exponential decay described by the equation V = V₀e^(-t/RC).
9. How would you modify this experiment to measure very small capacitances?
For very small capacitances, you might: use a higher initial charging voltage; use a very sensitive high-impedance voltmeter; reduce ambient temperature to increase leakage resistance; use shielded connections to minimize stray capacitance; employ a longer measurement time; or consider using alternative methods like bridge circuits that are more suitable for small capacitances.
10. Compare the leakage method with other methods of measuring capacitance. When would you prefer one over the other?
The leakage method is simple but time-consuming and is best for large capacitances with appreciable leakage. Bridge methods (like Schering bridge, De Sauty bridge) are more accurate but require more equipment and are good for precise measurements. Resonance methods are good for high-frequency applications. AC methods using impedance measurements are quick and common in modern instruments. The choice depends on the required accuracy, available equipment, capacitance range, and time constraints.

For More experiment Manual Click on Link...

There was an error loading the mathematical equations. Please refresh the page.
Scroll to Top