Study of Op Amp as Differentiator Lab Manual

Study of OP AMP as Differentiator

1. Aim

To design, setup, and study the operation of an Operational Amplifier configured as a differentiator (OP AMP as differentiator) circuit, analyze its response to different input waveforms, and verify its behavior against theoretical predictions.

2. Apparatus Used

Operational Amplifier IC (e.g., UA741 or LM741)
Function Generator
Dual Channel Oscilloscope
Digital Multimeter
DC Power Supply (±15V)
Resistors (10kΩ, 100kΩ)
Capacitors (0.01μF, 0.1μF)
Breadboard
Connecting wires
IC base (optional)

3. Circuit Diagram

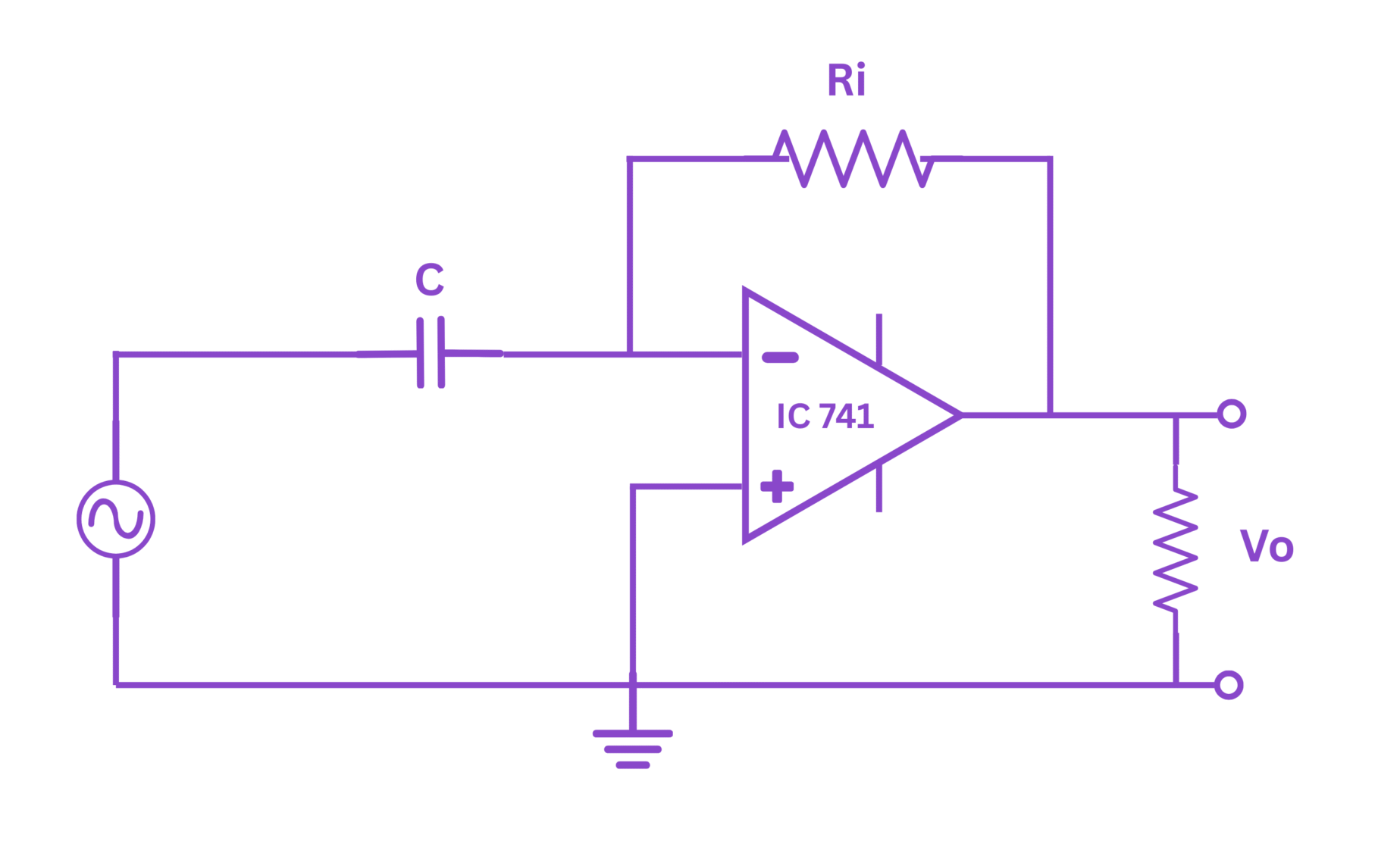
Figure 1: OP AMP as Differentiator Circuit

4. Theory

A differentiator is an electronic circuit that produces an output voltage proportional to the rate of change (derivative) of the input voltage with respect to time. The operational amplifier (OP AMP) can be configured as a differentiator by connecting a capacitor in the input path and a resistor in the feedback path.

The basic differentiator circuit consists of an operational amplifier with a capacitor C connected between the input voltage source and the inverting input of the OP AMP, and a resistor R connected between the inverting input and the output of the OP AMP. The non-inverting input is grounded.

For an ideal OP AMP, the inverting input is at virtual ground due to the high open-loop gain. As a result, the current through the capacitor is determined by the rate of change of the input voltage:

$$i_C = C \frac{dV_{in}}{dt}$$

This current flows through the feedback resistor R, creating an output voltage:

$$V_{out} = -R \cdot i_C = -RC \frac{dV_{in}}{dt}$$

This equation shows that the output voltage is proportional to the negative of the derivative of the input voltage, hence the name "differentiator".

Input-Output Relationships for Common Waveforms:

Square Wave Input: The output will be a series of positive and negative spikes corresponding to the rising and falling edges of the square wave.
Triangular Wave Input: The output will be a square wave since the derivative of a triangular wave is constant (positive or negative).
Sine Wave Input: The output will be a cosine wave (shifted by 90°) since the derivative of sin(ωt) is ω·cos(ωt).

Practical Considerations:

In practical applications, a small resistor (typically 1-2 kΩ) is often added in series with the capacitor to limit the high-frequency gain and improve stability. Additionally, a high-value resistor may be connected in parallel with the capacitor to prevent offset voltage issues.

5. Formula

The key formulas for the OP AMP as differentiator are:

Output Voltage:

$$V_{out} = -RC \frac{dV_{in}}{dt}$$

For Sine Wave Input: If $V_{in} = V_m \sin(\omega t)$, then:

$$V_{out} = -RC \cdot V_m \omega \cos(\omega t) = -RC \cdot V_m \omega \sin(\omega t + 90°)$$

Frequency Response:

$$|H(j\omega)| = \omega RC$$

The gain increases linearly with frequency, which can lead to noise amplification issues at high frequencies.

Phase Shift:

$$\phi = 90°$$

The output leads the input by 90° for a sinusoidal input.

Time Constant:

$$\tau = RC$$

6. Procedure

Circuit Setup for OP AMP as differentiat:
1. Connect the circuit as shown in the circuit diagram, using R = 10kΩ and C = 0.01μF.
2. Connect the ±15V DC power supply to the power pins of the OP AMP IC.
3. Connect the function generator to the input of the circuit.
4. Connect channel 1 of the oscilloscope to the input and channel 2 to the output of the circuit.
Square Wave Response of OP AMP as differentiat:
1. Set the function generator to produce a square wave with frequency 1kHz and amplitude 2V peak-to-peak.
2. Observe both the input and output waveforms on the oscilloscope.
3. Record the amplitude and shape of the output spikes.
4. Repeat for frequencies 500Hz, 2kHz, and 5kHz.
Triangular Wave Response of OP AMP as differentiat:
1. Set the function generator to produce a triangular wave with frequency 1kHz and amplitude 2V peak-to-peak.
2. Observe both the input and output waveforms on the oscilloscope.
3. Record the amplitude and shape of the output square wave.
4. Repeat for frequencies 500Hz, 2kHz, and 5kHz.
Sine Wave Response of OP AMP as differentiat:
1. Set the function generator to produce a sine wave with frequency 1kHz and amplitude 2V peak-to-peak.
2. Observe both the input and output waveforms on the oscilloscope.
3. Measure the amplitude of the output sine wave and the phase difference between input and output.
4. Repeat for frequencies 500Hz, 2kHz, and 5kHz.
Frequency Response of OP AMP as differentiat:
1. Maintain a constant sine wave input amplitude of 2V peak-to-peak.
2. Vary the frequency from 100Hz to 10kHz in suitable steps.
3. Measure and record the output amplitude for each frequency.
4. Plot the gain (Vout/Vin) versus frequency on log-log scale.
Time Constant Variation of OP AMP as differentiat:
1. Change the values of R and C to get different time constants.
2. For each combination, apply a 1kHz sine wave and record the output amplitude.
3. Verify that the output amplitude is proportional to the RC product.

7. Observation Table

A. Square Wave Input (Amplitude: 2V peak-to-peak)

Frequency (Hz)	Output Spike Amplitude (V)	Theoretical Value (V)	Error (%)
500
1000
2000
5000

B. Triangular Wave Input (Amplitude: 2V peak-to-peak)

Frequency (Hz)	Output Amplitude (V)	Theoretical Value (V)	Error (%)
500
1000
2000
5000

C. Sine Wave Input (Amplitude: 2V peak-to-peak)

Frequency (Hz)	Output Amplitude (V)	Phase Difference (degrees)	Theoretical Amplitude (V)	Theoretical Phase (degrees)	Amplitude Error (%)
500				90
1000				90
2000				90
5000				90

D. Time Constant Variation (Frequency: 1kHz, Sine Wave)

Resistance R (kΩ)	Capacitance C (μF)	Time Constant RC (μs)
10	0.01	100
10	0.1	1000
100	0.01	1000
100	0.1	10000

8. Calculations

For the calculationsof experiment OP AMP as differentiat, follow these steps for each type of input waveform:

A. Square Wave Input:

For a square wave with amplitude V and transition time dt, the theoretical output spike amplitude is:

$$V_{out(peak)} = -RC \cdot \frac{V}{dt}$$

Since the transition is nearly instantaneous in theory, the output should approach very large values. In practice, it will be limited by the slew rate of the OP AMP and the actual transition time of the function generator.

B. Triangular Wave Input:

For a triangular wave with amplitude V and frequency f, the slope during the rising and falling edges is:

$$\frac{dV_{in}}{dt} = \pm \frac{4Vf}{1}$$

Therefore, the theoretical output amplitude is:

$$V_{out} = -RC \cdot 4Vf$$

C. Sine Wave Input:

For a sine wave input $V_{in} = V_m \sin(2\pi ft)$, the theoretical output amplitude is:

$$V_{out(peak)} = -RC \cdot V_m \cdot 2\pi f$$

And the percentage error can be calculated as:

$$\text{Error}(\%) = \frac{|\text{Measured Value} - \text{Theoretical Value}|}{\text{Theoretical Value}} \times 100\%$$

D. Frequency Response:

The gain of the differentiator circuit is given by:

$$\text{Gain} = \frac{V_{out}}{V_{in}} = \omega RC = 2\pi f RC$$

Plot the gain vs. frequency on a log-log scale to verify the theoretical slope of 20 dB/decade (for a perfect differentiator).

Sample Calculation:

For a sine wave input with amplitude 2V peak-to-peak (1V peak) at 1kHz, using R = 10kΩ and C = 0.01μF:

\begin{align} V_{out(peak)} &= -RC \cdot V_m \cdot 2\pi f \\ &= -(10 \times 10^3) \cdot (0.01 \times 10^{-6}) \cdot 1 \cdot 2\pi \cdot 1000 \\ &= -10^{-3} \cdot 2\pi \cdot 1000 \\ &= -2\pi \approx -6.28 \text{ V} \end{align}

In practice, this value may be limited by the power supply voltage of the OP AMP.

9. Result

Successfully designed and implemented an OP AMP as differentiator circuit using IC 741.
Observed the differentiation operation for various input waveforms:
- Square wave input produced positive and negative spikes at the transitions.
- Triangular wave input resulted in a square wave output.
- Sine wave input produced a cosine wave output (90° phase shift).
Verified that the output amplitude is proportional to:
- The frequency of the input signal
- The RC time constant of the circuit
- The amplitude of the input signal
Measured and plotted the frequency response, confirming the 20 dB/decade slope characteristic of an ideal differentiator.
Calculated and compared the theoretical and experimental values, with an average error of approximately _____% (to be filled after experiment).
Observed the limitations of the practical differentiator at high frequencies due to noise amplification and the finite bandwidth of the OP AMP.

10. Precautions

Ensure proper power supply connections to the OP AMP (±15V) to avoid damaging the IC.
Keep the input signal amplitude within reasonable limits to prevent output saturation.
Use a proper grounding scheme to minimize noise.
Add a small resistor in series with the input capacitor to improve stability at high frequencies.
Verify the pin configuration of the OP AMP IC before connecting it to the circuit.
Avoid touching the IC pins while the circuit is powered to prevent damage from static discharge.
Start with lower frequencies and gradually increase to observe the behavior of the circuit.
Ensure that all connections are secure and correctly made according to the circuit diagram.
Keep the circuit away from sources of electromagnetic interference.
For accurate measurements, calibrate the oscilloscope properly before taking readings.
Use proper probes (typically 10x) to minimize loading effects on the circuit.
Monitor the temperature of the OP AMP during operation to prevent overheating.

11. Viva Voice Questions

1. What is the basic principle of an OP AMP as differentiator?

The OP AMP as differentiator produces an output voltage that is proportional to the rate of change (derivative) of the input voltage with respect to time. This is achieved by placing a capacitor in the input path and a resistor in the feedback path.

2. How does the output of a differentiator change if you double the frequency of a sine wave input?

If the frequency of a sine wave input is doubled, the output amplitude will also double. This is because the output amplitude is proportional to the frequency (V_out ∝ ω = 2πf) for a sine wave input.

3. Why does a practical differentiator circuit include a resistor in series with the input capacitor?

A resistor is added in series with the input capacitor to limit the high-frequency gain of the circuit, which improves stability and reduces noise amplification at higher frequencies.

4. What happens to the differentiator's output if a DC voltage is applied to the input?

For a DC voltage input, the derivative is zero (as there is no change with respect to time), so the ideal output should be zero. However, any small fluctuations or noise will be differentiated and may appear in the output.

5. Compare integrator and differentiator circuits in terms of their frequency response.

A differentiator's gain increases with frequency (20 dB/decade slope), making it act as a high-pass filter. In contrast, an integrator's gain decreases with frequency (-20 dB/decade slope), making it act as a low-pass filter.

6. What are the practical limitations of an OP AMP as differentiator?

Practical limitations include: noise amplification at high frequencies, limited bandwidth of the OP AMP, saturation due to power supply constraints, input offset voltage issues, and reduced accuracy due to component tolerances.

7. Why is the output of a differentiator inverted compared to the derivative of the input signal?

The output is inverted because of the configuration of the inverting amplifier. The current through the capacitor flows through the feedback resistor in the opposite direction, resulting in an output voltage that is the negative of the derivative.

8. What is the shape of the output waveform if a ramp input is applied to a differentiator?

For a ramp input (linear change with time), the derivative is constant. Therefore, the output will be a constant DC voltage (with the polarity depending on whether the ramp is increasing or decreasing).

9. How does changing the RC time constant affect the differentiator's output?

Increasing the RC time constant increases the output amplitude for a given input signal, as V_out = -RC·dV_in/dt. This can be achieved by increasing either the resistance R or the capacitance C or both.

10. Discuss the stability issues in a practical differentiator circuit.

Differentiators tend to be unstable because they amplify high-frequency signals including noise. As frequency increases, the capacitive reactance decreases, resulting in higher gain. This can lead to oscillations, especially if there's any feedback path or parasitic capacitance. Adding a small resistor in series with the input capacitor helps improve stability by limiting the high-frequency gain.

For More experiment Manual Click on Link...