To find the number of lines per centimeter of the given diffraction grating
To determine the number of lines per centimeter of the given diffraction grating using a spectrometer and mercury vapor lamp.
For measuring angles of diffracted light
The grating whose line density is to be found
Source of monochromatic light
For precise reading of scale
For leveling the spectrometer
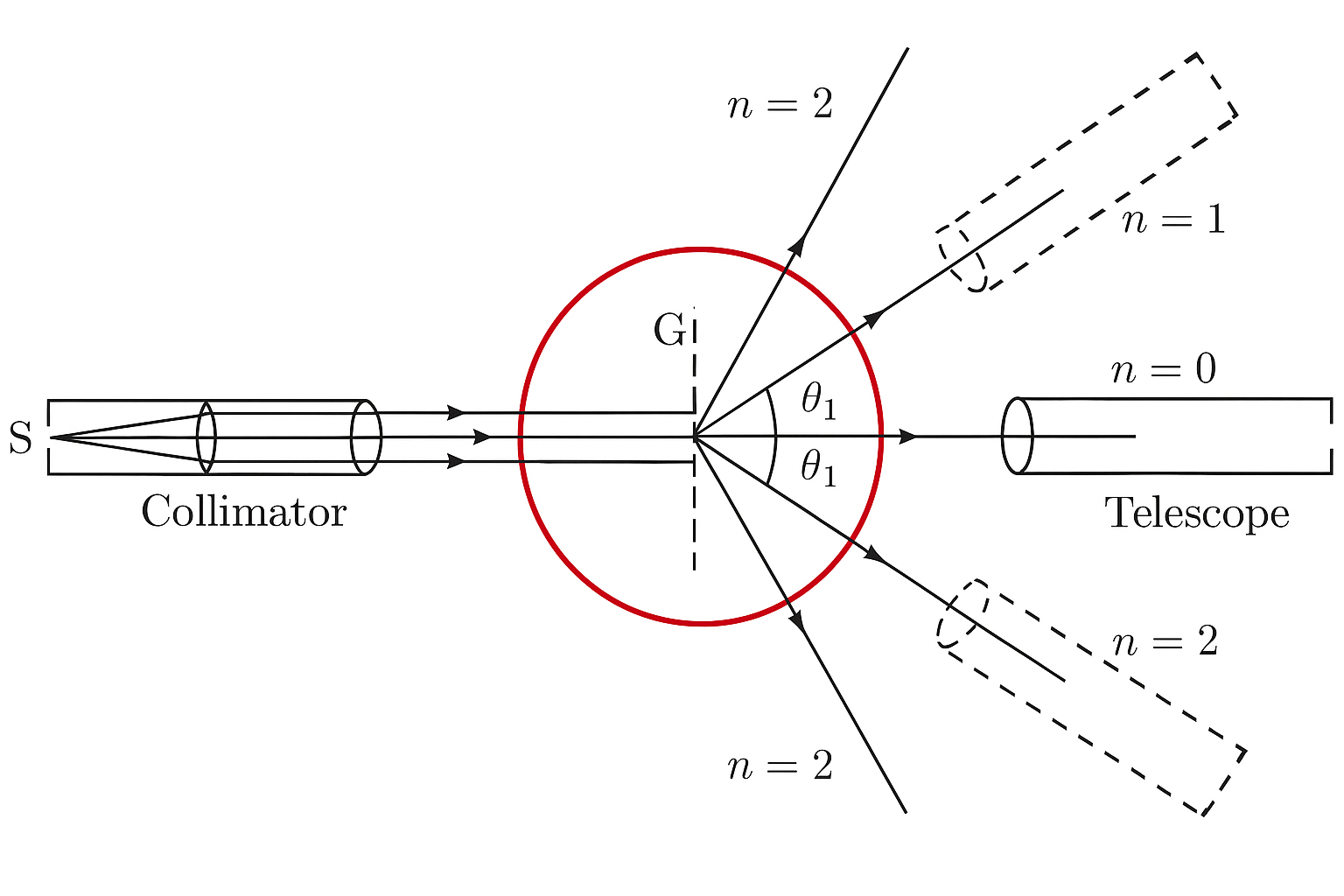
A diffraction grating consists of a large number of parallel slits of equal width separated by equal distances. When monochromatic light is incident on a diffraction grating, it produces a series of bright and dark fringes due to interference of light waves diffracted by different slits.
The condition for constructive interference (bright fringes) is given by the grating equation. For normal incidence, when light falls perpendicularly on the grating, the path difference between rays from adjacent slits is d sin θ, where d is the grating spacing and θ is the angle of diffraction.
For constructive interference, this path difference must be an integral multiple of the wavelength. The intensity of diffracted light depends on both the number of slits and their individual diffraction patterns.
Mercury vapor lamp provides several distinct spectral lines, with the green line (λ = 546.1 nm) being most prominent and suitable for measurements.
Where:
- d = grating spacing (distance between adjacent slits)
- θ = angle of diffraction
- n = order of diffraction (n = 0, ±1, ±2, ±3, ...)
- λ = wavelength of light
For mercury green line: λ = 546.1 nm = 5.461 × 10⁻⁵ cm
- Setup: Place the spectrometer on a stable table and level it using the spirit level and leveling screws.
- Collimator Adjustment: Adjust the collimator slit width and focus the eyepiece of the telescope to see clear, parallel light rays.
- Grating Mounting: Mount the diffraction grating vertically on the prism table with the ruled surface facing the collimator.
- Alignment: Rotate the prism table to make the grating surface perpendicular to the incident light from the collimator.
- Light Source: Place the mercury vapor lamp in front of the collimator and switch it on. Allow it to warm up for proper spectral line emission.
- Zero Order: Observe the direct (zero-order) spectrum through the telescope and note its position.
- First Order Measurement: Rotate the telescope to observe the first-order spectrum on one side. Record the angle reading.
- Symmetric Measurement: Rotate the telescope to the other side and record the first-order spectrum position on the opposite side.
- Higher Orders: If visible, repeat the measurements for second and third-order spectra.
- Data Recording: Record all angle measurements with proper precision in the observation table.
| Order of Diffraction (n) | Telescope Readings | Difference 2θ (degrees) |
θ (degrees) | sin θ | N = n/(λ sin θ) (lines/cm) |
|
|---|---|---|---|---|---|---|
| Left Side (degrees) |
Right Side (degrees) |
|||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
Note: λ (mercury green line) = 546.1 nm = 5.461 × 10⁻⁵ cm
Step 1: Calculate the diffraction angle
$$\theta = \frac{\text{Difference in telescope readings}}{2}$$Step 2: Calculate sin θ
$$\sin \theta = \sin\left(\frac{\text{2θ}}{2}\right)$$Step 3: Apply the grating equation
$$N = \frac{n}{\lambda \sin \theta}$$Step 4: Convert to lines per cm
$$N = \frac{n}{5.461 \times 10^{-5} \times \sin \theta} \text{ lines/cm}$$Mean Value: Calculate the average number of lines per centimeter from different orders of diffraction to get the final result.
The number of lines per centimeter of the given diffraction grating = _______ lines/cm
Percentage Error: If standard value is known, calculate percentage error using:
A: A diffraction grating is an optical device consisting of many parallel slits that diffracts light into several beams traveling in different directions. It works on the principle of interference of light waves.
A: Transmission grating allows light to pass through it while reflection grating reflects the incident light. Both produce diffraction patterns but on opposite sides.
A: Mercury vapor lamp provides distinct monochromatic spectral lines with known wavelengths, particularly the prominent green line at 546.1 nm.
A: Increasing the number of slits makes the bright fringes sharper and more intense while the dark regions become darker.
A: Higher-order spectra (n = 2, 3, ...) appear at larger angles and provide additional data points for calculating grating constant with better accuracy.
A: Diffraction grating provides better resolution, linear dispersion, and can separate closely spaced wavelengths more effectively than a prism.
A: Resolving power is the ability of a grating to distinguish between two closely spaced wavelengths. It is given by R = λ/Δλ = nN, where N is total number of lines.
A: Taking readings from both sides helps eliminate errors due to misalignment of optical axis and provides more accurate angle measurements.
