Conical Pendulum Simulation
"Interactive conical pendulum simulation. Adjust length, angle, mass & gravity. Visualizes circular motion, calculates period, tension & forces. Perfect for physics ed!"
Conical Pendulum Simulation
Conical Pendulum Simulation Guide
Getting Started: Click "Start" to begin the simulation with default values.
Controls:
- Adjust sliders to change parameters
- Use "Pause" to freeze the motion
- "Reset" returns to initial conditions
- "Clear Path" removes the trajectory trail
Experiment Ideas:
- Change the string length and observe period changes
- Increase the angle to see how tension increases
- Reduce gravity to simulate lunar conditions
- Adjust perspective to understand the elliptical appearance
Conical Pendulum Physics
A conical pendulum consists of a mass (bob) suspended from a fixed point that moves in a horizontal circular path. The string traces out a cone, hence the name.
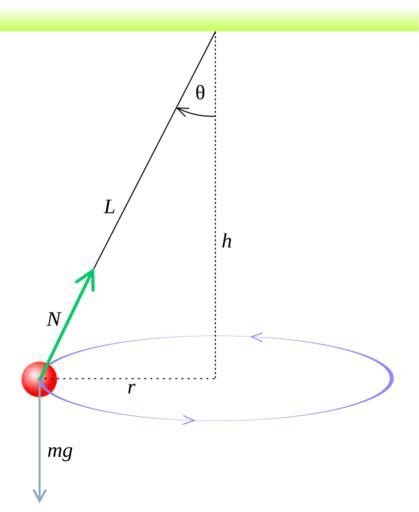
Key Concepts:
- The vertical component of tension balances gravity (Tcosθ = mg)
- The horizontal component provides centripetal force (Tsinθ = mv²/r)
- The period is independent of mass for small angles
- The path appears elliptical due to perspective effects
Control Panel
Adjust the pendulum's string length (0.5m to 3m)
Change the angle between string and vertical (10° to 80°)
Modify the mass of the pendulum bob (0.1kg to 2kg)
Simulate different gravitational environments (1m/s² to 20m/s²)
Change viewing angle to understand the elliptical path
Key Formulas:
Radius: r = L·sin(θ)
Period: T = 2π√(L·cos(θ)/g)
Angular Velocity: ω = √(g/(L·cosθ))
Tension: T = mg/cos(θ)
In-Depth Theory
Historical Context
The conical pendulum was first studied by Robert Hooke in the 17th century as he investigated circular motion. Later, it became important in demonstrating the Earth's rotation through Foucault's pendulum variations.
Mathematical Derivation
For a conical pendulum with string length L and angle θ:
- Vertical equilibrium: Tcosθ = mg
- Horizontal (centripetal) force: Tsinθ = mω²(Lsinθ)
- Combining gives: ω = √(g/(Lcosθ))
- Period T = 2π/ω = 2π√(Lcosθ/g)
Real-world Applications
- Centrifuges: Operating on similar principles to separate materials
- Amusement rides: Many spinning rides use conical pendulum physics
- Sports: Analysis of hammer throw and other rotational sports
- Earth science: Demonstrating Coriolis effects
Common Misconceptions
- The mass affects tension but not period (for small angles)
- The circular motion isn't perfect in reality due to air resistance
- The elliptical appearance is purely a perspective effect
Simulation Results
| Parameter | Value | Description |
|---|---|---|
| Period (T) | - | Time for one complete revolution |
| Angular Velocity (ω) | - | Rotation rate in radians per second |
| Linear Velocity (v) | - | Bob's tangential speed |
| Radius (r) | - | Horizontal circle radius |
| Tension | - | Force in the string |
| Centripetal Force | - | Net inward force |
Energy Analysis
| Energy Type | Value |
|---|---|
| Potential Energy | - |
| Kinetic Energy | - |
| Total Mechanical Energy | - |
Energy Formulas:
PE = mgh = mgL(1-cosθ)
KE = ½mv² = ½m(ωLsinθ)²
