Determination of Acceleration Due to Gravity Using Simple Pendulum
Click here to perform experiment with simple pendulum simulation1. Aim
To determine the acceleration due to gravity (g) at a place by using a simple pendulum and to study the relationship between the length of the pendulum and its time period.
2. Apparatus Used
- Small heavy metallic bob
- Fine, inextensible string (about 1-1.5m long)
- Retort stand with clamp
- Stopwatch (least count 0.1s)
- Meter scale (least count 1mm)
- Vernier calipers (to measure bob diameter)
- Split cork or knife edge for suspension
3. Diagram
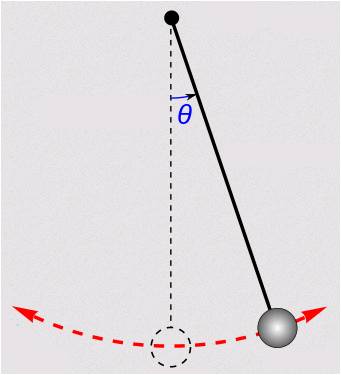
Figure: Simple pendulum showing length (l), bob diameter (d), and angular displacement (θ)
4. Theory
A simple pendulum consists of a point mass suspended by a weightless, inextensible string from a rigid support. When displaced from its mean position and released, it executes simple harmonic motion (for small angles θ ≤ 5°).
The time period (T) of oscillation of a simple pendulum is given by:
Where:
- \( T \) = Time period of oscillation
- \( L \) = Effective length of pendulum (string length + radius of bob)
- \( g \) = Acceleration due to gravity
Rearranging the formula gives the expression for g:
For small oscillations (θ ≤ 5°), the time period is independent of:
- Mass of the bob
- Amplitude of oscillation
5. Formula
The acceleration due to gravity is calculated using:
Where:
- Effective length \( L = l + r \)
\[ l = \text{length of string} \] \[ r = \text{radius of bob} = \frac{d}{2} \]
- Time period \( T = \frac{\text{Time for n oscillations}}{n} \)
6. Procedure
- Measure the diameter (d) of the bob using vernier calipers and calculate radius (r = d/2).
- Set up the pendulum by suspending the bob with the string from the rigid support.
- Adjust the length (l) of the string to about 50 cm (from point of suspension to top of bob).
- Measure the exact length (l) using the meter scale.
- Calculate effective length: \( L = l + r \).
- Displace the bob slightly (≤ 5°) and release to start oscillations.
- Measure time for 20 oscillations using stopwatch and calculate time period (T).
- Repeat the measurement for the same length 3 times and take average T.
- Repeat steps 3-8 for different lengths (e.g., 60cm, 70cm,..., 100cm).
- Record all observations in the tabular form.
- Plot graph of \( T^2 \) vs L and determine g from the slope.
7. Observation Table
| S.No. | Length of string (l) in cm | Effective length L = l + r (cm) | Time for 20 oscillations (s) | Mean Time Period T (s) | \( T^2 \) (s²) | ||
|---|---|---|---|---|---|---|---|
| Trial 1 | Trial 2 | Trial 3 | |||||
| 1 | 50.0 | ||||||
| 2 | 60.0 | ||||||
| 3 | 70.0 | ||||||
| 4 | 80.0 | ||||||
| 5 | 90.0 | ||||||
| 6 | 100.0 | ||||||
Diameter of bob (d) = _____ cm
Radius of bob (r = d/2) = _____ cm
8. Calculations
- For each length, calculate effective length:
\[ L = l + r \]
- Calculate mean time period for each length:
\[ T = \frac{\text{Mean time for 20 oscillations}}{20} \]
- Calculate \( T^2 \) for each length.
- Plot graph of \( T^2 \) (y-axis) vs L (x-axis). The graph should be a straight line.
- Determine slope (m) of the graph:
\[ m = \frac{\Delta T^2}{\Delta L} \]
- Calculate g using:
\[ g = 4\pi^2 \frac{1}{m} \]
- Alternatively, calculate g for each length using:
\[ g = 4\pi^2 \frac{L}{T^2} \]and take average.
Graph Plotting Instructions
Plot \( T^2 \) (y-axis) vs L (x-axis):
- The graph should be a straight line passing through origin
- Determine slope using two distant points on the line
- Calculate g from the inverse of the slope
9. Result
- The acceleration due to gravity (g) determined from the experiment = _____ m/s²
- Standard value of g at the location = _____ m/s²
- Percentage error = _____ %
- The graph of \( T^2 \) vs L is a straight line, verifying \( T \propto \sqrt{L} \) relationship
10. Precautions
- Ensure the string is inextensible and the support is rigid
- Amplitude of oscillation should be small (≤ 5°)
- Time at least 20 oscillations to reduce timing errors
- Measure length from point of suspension to center of bob
- Avoid air currents that may affect oscillations
- Repeat measurements for each length to minimize errors
- Start and stop stopwatch at the mean position
- Ensure oscillations are in one plane without rotation
