TO DRAW THE MAGNETIC LINES OF FORCE DUE TO A BAR MAGNET
1. AIM
2. APPARATUS USED
- A bar magnet
- A magnetic compass
- Drawing board
- Drawing sheet (white paper)
- Drawing pins or adhesive tape
- Pencil (HB)
- Scale and protractor
3. DIAGRAM
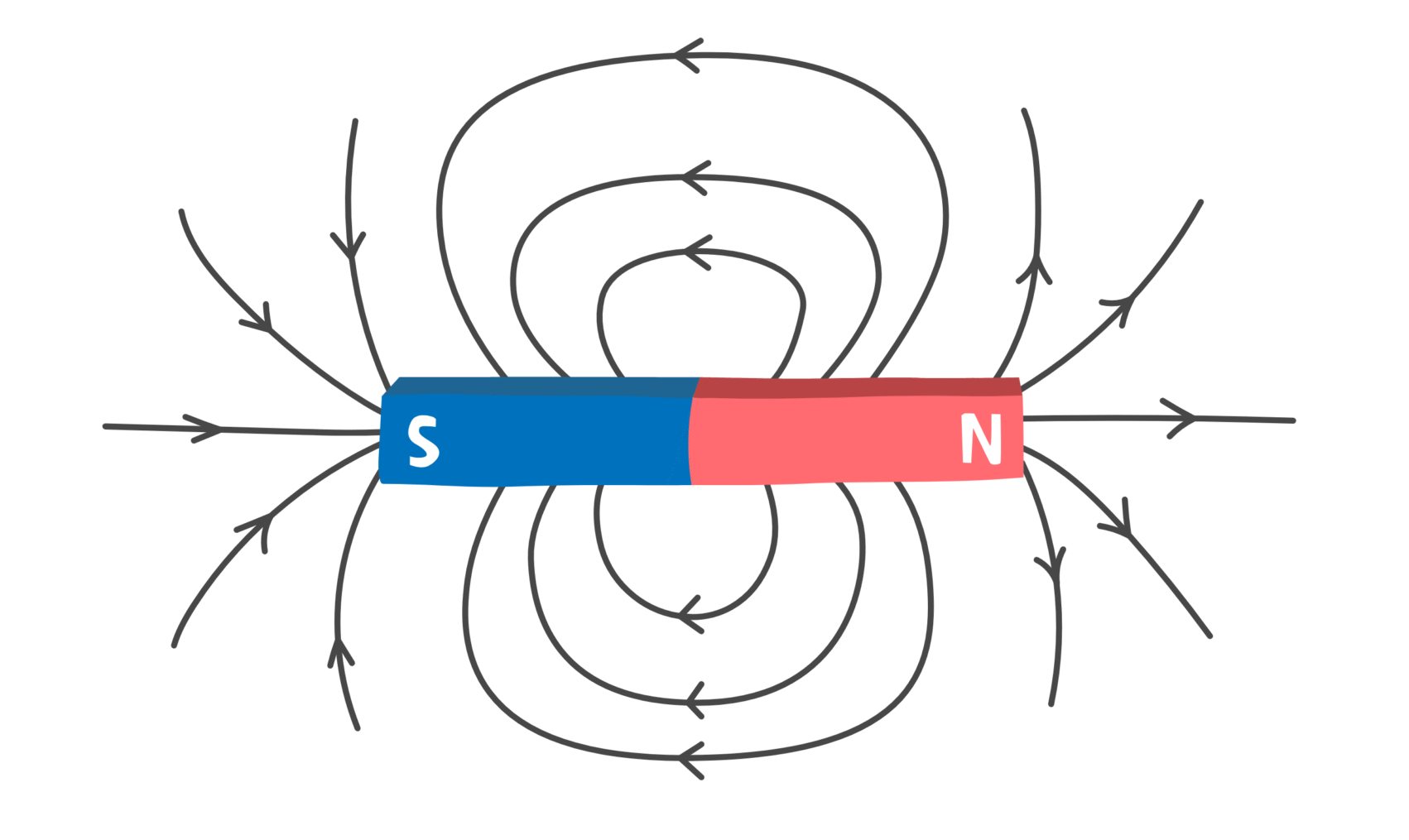
Fig. 1: Magnetic field lines around a bar magnet
4. THEORY
A magnet is surrounded by a magnetic field that exerts forces on other magnetic materials or moving charges. This field can be represented by magnetic lines of force, which are imaginary lines used to visualize the direction and strength of the magnetic field.
The magnetic lines of force have the following properties:
- They originate from the north pole and terminate at the south pole of the magnet.
- The tangent to a field line at any point gives the direction of the magnetic field at that point.
- The density of the lines indicates the strength of the magnetic field; closer lines mean a stronger field.
- The lines never intersect each other.
- Outside the magnet, they travel from north to south pole, while inside the magnet, they travel from south to north pole, forming closed loops.
The magnetic field at any point due to a bar magnet can be represented mathematically. For a point at a distance $r$ from the center of a magnet making an angle $\theta$ with the axis of the magnet, the magnetic field has two components:
where $B_r$ is the radial component, $B_\theta$ is the transverse component, $\mu_0$ is the permeability of free space, and $M$ is the magnetic moment of the bar magnet.
Neutral Points: These are points in the magnetic field where the resultant field is zero. For a bar magnet, they are located along the axial line and equatorial line, where the magnetic field of the magnet exactly cancels the earth's magnetic field.
5. FORMULA
The magnetic field at a distance $r$ from the center of a magnetic dipole of moment $M$ is given by:
Where:
- $B$ is the magnetic field strength at the point
- $\mu_0$ is the permeability of free space ($4\pi \times 10^{-7}$ H/m)
- $M$ is the magnetic moment of the bar magnet
- $r$ is the distance from the center of the magnet to the point of observation
- $\theta$ is the angle made by the line joining the center of the magnet and the point of observation with the axis of the magnet
For the axial line ($\theta = 0°$ or $180°$):
For the equatorial line ($\theta = 90°$):
6. PROCEDURE
- Preparation:
- Fix a white paper on the drawing board using drawing pins or adhesive tape.
- Place the bar magnet at the center of the paper.
- Mark the outline of the bar magnet on the paper.
- Label the north and south poles of the magnet clearly.
- Tracing Magnetic Field Lines:
- Place the magnetic compass near one pole of the bar magnet.
- Mark a dot at the position of the pointer of the compass needle.
- Move the compass such that the tail of the needle coincides with the previously marked dot.
- Mark another dot at the position of the pointer.
- Continue this process until you reach the other pole of the magnet.
- Join all the dots with a smooth curve to get one magnetic line of force.
- Repeat the procedure to draw several magnetic lines of force by starting from different positions around one pole.
- Locating Neutral Points:
- Place the magnet such that its north pole points towards the geographic north.
- Move the compass slowly along the axial line on both sides of the magnet.
- Look for positions where the compass needle becomes unstable or rotates freely.
- Mark these positions as neutral points.
7. OBSERVATION TABLE
Field Line Measurements:
| Line No. | Starting Position (from N-pole) | Points Marked (coordinates in cm) | Field Direction |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Neutral Points:
| Neutral Point | Position (x, y) in cm | Distance from Center of Magnet (cm) |
|---|---|---|
| 1 | ||
| 2 |
8. CALCULATIONS
1. Calculating Field Strength at Different Points:
For any point at a distance $r$ from the center of the magnet, the magnetic field strength can be calculated using:
2. Verifying Inverse Cube Law:
Plot a graph of field strength ($B$) versus distance ($r$). If the law is followed, the graph of $B$ vs $\frac{1}{r^3}$ should be a straight line.
3. Calculating Magnetic Moment:
If the field strength at a known point is measured, the magnetic moment can be calculated by rearranging the formula:
4. Locating Neutral Points:
For a bar magnet placed in the Earth's magnetic field, the neutral points occur where:
Where $B_E$ is the horizontal component of Earth's magnetic field.
This can be rearranged to find the theoretical distance of neutral points:
9. RESULT
- The magnetic lines of force around the bar magnet were successfully traced.
- The magnetic field lines form closed loops that emerge from the north pole and enter the south pole.
- The field lines are closer near the poles indicating stronger magnetic field in those regions.
- The neutral points were located at a distance of approximately _____ cm from the center of the magnet.
- The pattern of the magnetic field lines demonstrates that the magnetic field follows the inverse cube law.
10. PRECAUTIONS
- Keep the bar magnet away from other magnetic materials during the experiment.
- Ensure that the drawing board is horizontal and free from vibrations.
- The compass needle should be free to rotate without any friction.
- Mark the outline of the magnet accurately on the paper.
- When tracing a field line, ensure that the tail of the compass needle exactly coincides with the previously marked dot.
- Keep electronic devices away from the experimental setup as they may interfere with the magnetic field.
- Handle the bar magnet carefully to avoid demagnetization due to dropping or heating.
- Use a small compass to get more accurate results, especially near the poles where the field lines are dense.
- Take readings at shorter intervals near the poles for better accuracy.
- Do not move the paper or the magnet once the experiment has started.
11. VIVA VOICE QUESTIONS
Q1: What are magnetic lines of force?
A1: Magnetic lines of force are imaginary lines used to visualize the direction and strength of a magnetic field. The tangent to a line at any point gives the direction of the magnetic field at that point, and the density of the lines indicates the field strength.
Q2: Why do magnetic lines of force never intersect each other?
A2: Magnetic lines of force never intersect because if they did, it would mean that at the point of intersection, the magnetic field has two different directions simultaneously, which is physically impossible. The magnetic field can have only one definite direction at any given point in space.
Q3: What is a neutral point in a magnetic field?
A3: A neutral point is a location in space where the net magnetic field is zero. In the context of a bar magnet placed in the Earth's magnetic field, neutral points occur where the magnetic field of the bar magnet exactly cancels the Earth's magnetic field.
Q4: How does the magnetic field strength vary with distance from a bar magnet?
A4: The magnetic field strength of a bar magnet varies inversely as the cube of the distance from the center of the magnet. This relationship is known as the inverse cube law ($B \propto \frac{1}{r^3}$).
Q5: Why are the magnetic field lines crowded near the poles of a magnet?
A5: The magnetic field lines are crowded near the poles because the magnetic field strength is greatest near the poles. The density of field lines is proportional to the strength of the magnetic field, so more lines per unit area indicates a stronger field.
Q6: What happens to the magnetic field lines inside a bar magnet?
A6: Inside the bar magnet, the magnetic field lines travel from the south pole to the north pole, forming closed loops with the external field lines that go from north to south outside the magnet.
Q7: How would the pattern of magnetic field lines change if you break a bar magnet into two pieces?
A7: If a bar magnet is broken into two pieces, each piece becomes a complete magnet with its own north and south poles. The pattern of field lines around each piece would be similar to that of the original magnet, but scaled accordingly to the size and strength of each new magnet.
Q8: What is the difference between magnetic field lines of a bar magnet and an electric dipole?
A8: While both patterns look similar, magnetic field lines form closed loops (no beginning or end), whereas electric field lines start from positive charges and end at negative charges. Also, magnetic monopoles don't exist, but electric monopoles (isolated charges) do.
Q9: How does the Earth's magnetic field interact with the magnetic field of a bar magnet?
A9: The Earth's magnetic field interacts with the magnetic field of a bar magnet through superposition. The resultant field at any point is the vector sum of the Earth's field and the bar magnet's field. This interaction leads to the formation of neutral points where these fields cancel each other out.
Q10: What are the factors that affect the magnetic field strength of a bar magnet?
A10: The factors affecting the magnetic field strength include: the material of the magnet (its permeability), the size and shape of the magnet, the temperature (heating typically reduces magnetization), the presence of other magnetic materials nearby, and the distance from the magnet (field strength decreases with increasing distance).
