DETERMINATION OF MAGNETIC SUSCEPTIBILITY OF LIQUID BY QUINCKE'S METHOD
To determine the magnetic susceptibility of a paramagnetic liquid using Quincke's method
.- Quincke's tube apparatus (U-shaped glass tube with one limb of larger diameter)
- Electromagnet
- Traveling microscope or cathetometer
- Ammeter (0-5 A)
- Rheostat
- Battery or DC power supply
- Paramagnetic liquid sample (e.g., MnSO₄ solution, FeCl₃ solution)
- Connecting wires
- Key/Switch
- Gaussian meter or Hall probe (for measuring magnetic field)
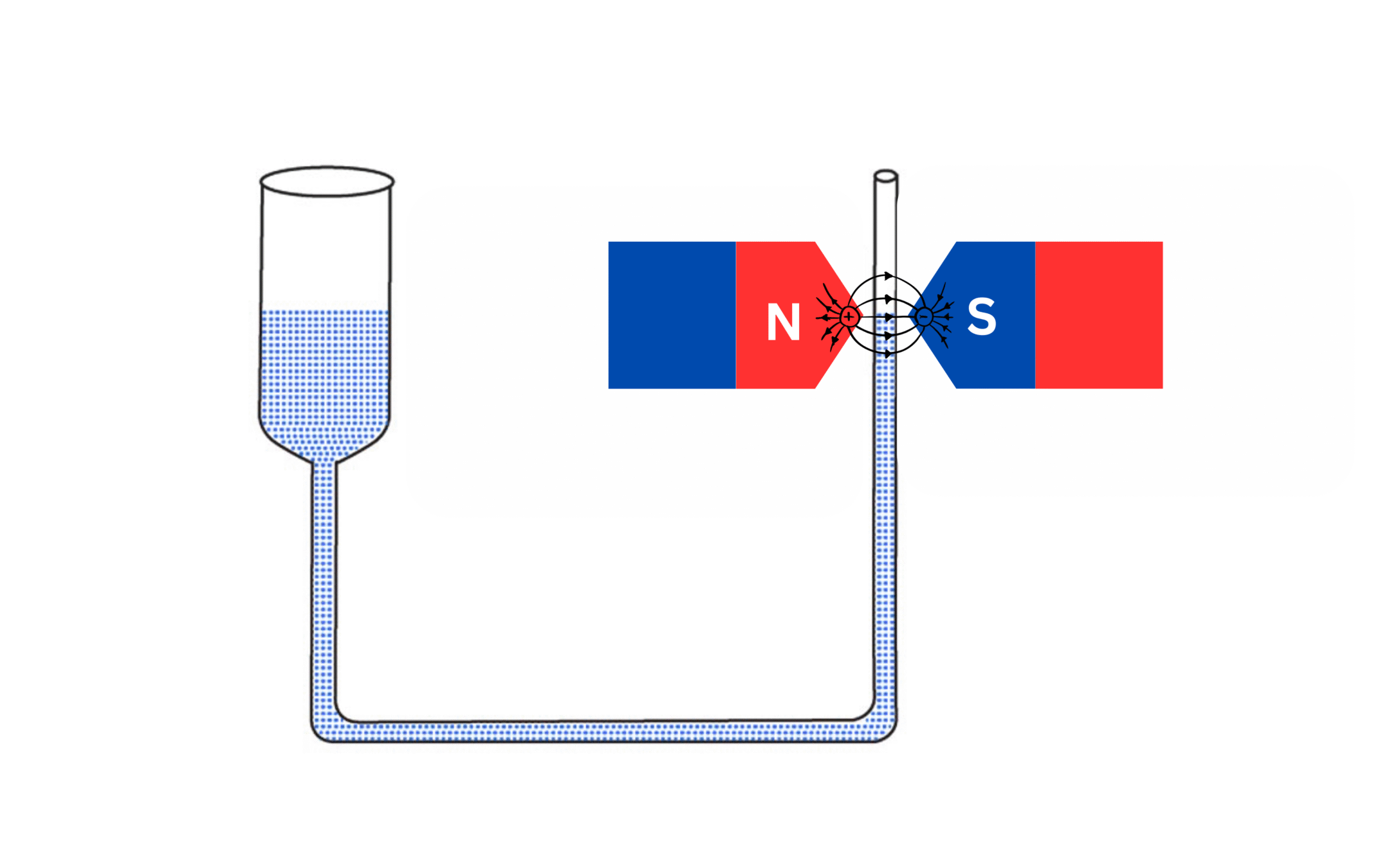
Fig. 1: Experimental setup for Magnetic Susceptibility using Quincke's method
Quincke's method is used to determine the magnetic susceptibility of paramagnetic liquids. This method is based on the principle that when a paramagnetic liquid is placed in a non-uniform magnetic field, it experiences a force in the direction of increasing field strength.
When a U-tube containing the paramagnetic liquid is placed between the poles of an electromagnet such that one limb is in the uniform field region and the other limb is in a region where the field is non-uniform or zero, the liquid rises in the limb placed in the stronger field.
The rise in liquid level is due to the force experienced by the liquid in the direction of the stronger field. This force arises from the interaction between the induced magnetic moment in the liquid and the gradient of the magnetic field.
For a paramagnetic liquid with volume magnetic susceptibility χ, the force per unit volume in a non-uniform magnetic field is given by:
\( F_v = \frac{\chi H}{2\mu_0} \frac{dH}{dx} \)
Where:
- \( F_v \) is the force per unit volume
- \( \chi \) is the volume magnetic susceptibility
- \( H \) is the magnetic field intensity
- \( \mu_0 \) is the permeability of free space
- \( \frac{dH}{dx} \) is the gradient of the magnetic field
This force causes a difference in the height of the liquid in the two limbs of the U-tube. The equilibrium is reached when the magnetic force is balanced by the hydrostatic pressure difference due to the height difference.
The relationship between the height difference and the magnetic susceptibility is given by:
\( \chi = \frac{2\mu_0\rho g h}{B^2} \)
Where:
- \( \chi \) is the volume magnetic susceptibility of the liquid
- \( \mu_0 \) is the permeability of free space (\( 4\pi \times 10^{-7} \) H/m)
- \( \rho \) is the density of the liquid (kg/m³)
- \( g \) is the acceleration due to gravity (9.8 m/s²)
- \( h \) is the difference in height of the liquid in the two limbs (m)
- \( B \) is the magnetic field strength (T)
Alternatively, the formula can be expressed as:
\( \chi = \frac{2\rho g h}{\mu_0 H^2} \)
Where \( H \) is the magnetic field intensity in A/m.
- Set up the apparatus as shown in the diagram, with the Quincke's tube placed such that one limb is between the poles of the electromagnet and the other limb is away from the magnetic field.
- Ensure that the U-tube is clean and dry.
- Fill the U-tube with the paramagnetic liquid sample up to a convenient height.
- Adjust the tube so that the liquid levels in both limbs are equal when no magnetic field is applied.
- Note the initial position of the liquid level in both limbs using the traveling microscope or cathetometer.
- Switch on the electromagnet and gradually increase the current using the rheostat.
- Note the current value from the ammeter.
- Measure the magnetic field strength using a Gaussian meter or Hall probe at the position of the limb placed in the field.
- Observe the rise of the liquid in the limb placed in the magnetic field.
- When the liquid levels stabilize, measure the new positions of the liquid levels in both limbs.
- Calculate the difference in height (h) between the two limbs.
- Repeat the experiment for different values of the magnetic field strength by varying the current through the electromagnet.
- Switch off the electromagnet and observe that the liquid levels return to their initial equal positions.
- Record all observations in the observation table.
- Calculate the magnetic susceptibility using the appropriate formula.
| S.No. | Current through electromagnet (A) | Magnetic field (B) (Tesla) | Initial position of liquid level (mm) | Final position of liquid level (mm) | Height difference (h) (mm) | Calculated susceptibility (χ) |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
Using the formula:
\( \chi = \frac{2\mu_0\rho g h}{B^2} \)
Sample calculation for the first observation:
Given:
- Density of the liquid (ρ) = ___ kg/m³
- Gravitational acceleration (g) = 9.8 m/s²
- Height difference (h) = ___ m
- Magnetic field strength (B) = ___ T
- Permeability of free space (μ₀) = 4π × 10⁻⁷ H/m
Substituting these values in the formula:
\( \chi = \frac{2 \times 4\pi \times 10^{-7} \times \rho \times 9.8 \times h}{B^2} \)
= (Calculate the numerical value)
The mean value of the magnetic susceptibility from all observations is:
\( \chi_{mean} = \frac{\chi_1 + \chi_2 + \chi_3 + \chi_4 + \chi_5}{5} \)
The magnetic susceptibility of the given paramagnetic liquid (name of the liquid) as determined by Quincke's method is ________ (with appropriate unit).
- The U-tube should be thoroughly cleaned and dried before filling with the liquid.
- Ensure that no air bubbles are trapped in the liquid.
- The magnetic field should be uniform across the limb placed in the field.
- Avoid parallax error while taking readings of liquid levels.
- Ensure that the experiment is performed in a vibration-free environment.
- Take readings only after the liquid levels have stabilized.
- The temperature of the liquid should remain constant throughout the experiment.
- The U-tube should be perfectly vertical.
- Ensure that there are no magnetic materials near the experimental setup.
- The electromagnet should be properly cooled to avoid overheating.
