2
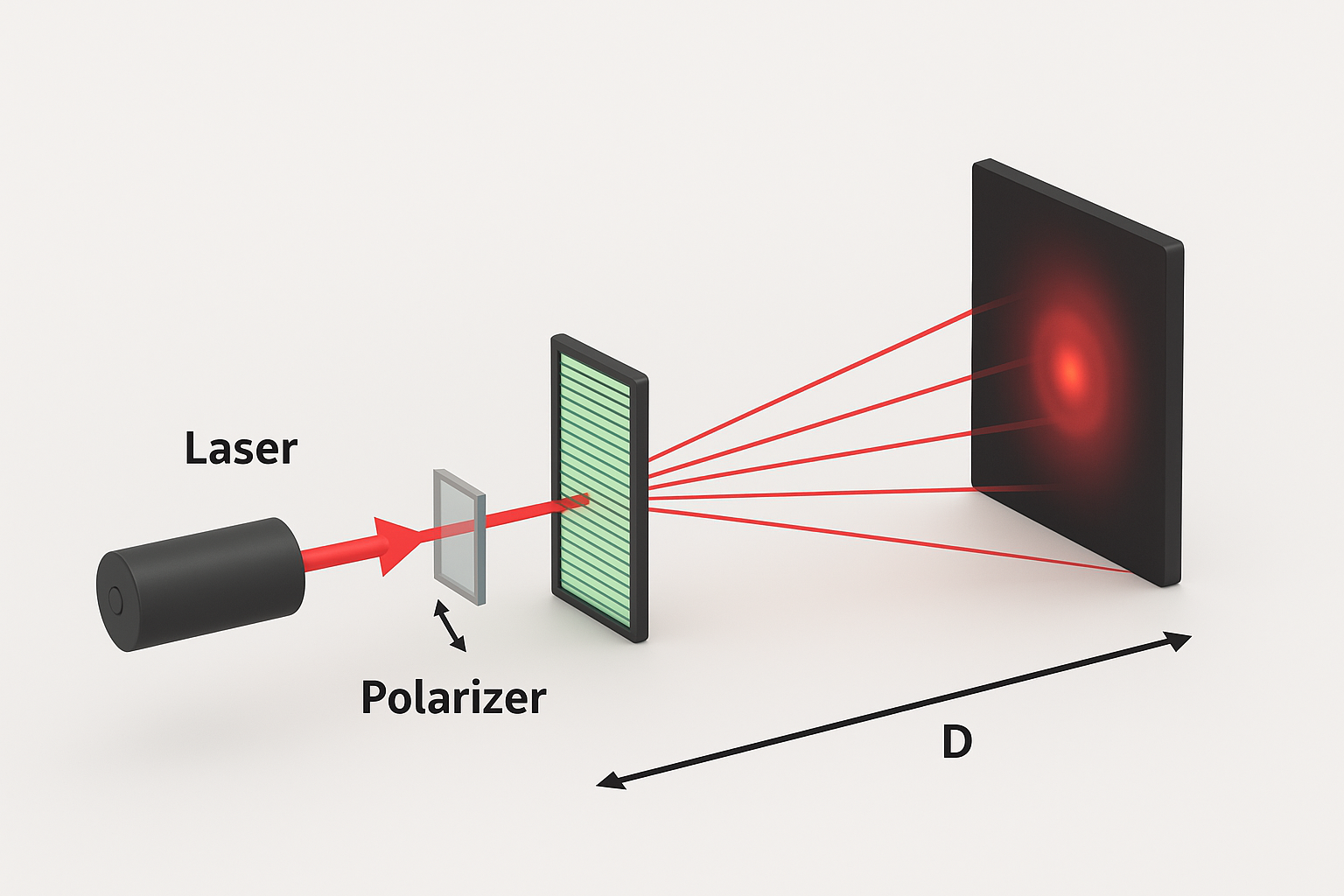
Apparatus Used
Laser Source: He-Ne laser or diode laser (wavelength ~630-650 nm)
Diffraction Grating: Plane transmission grating (300-600 lines/mm)
Screen: White screen or wall for observing diffraction pattern
Measuring Scale: Meter scale or measuring tape
Optical Bench: For mounting and alignment of components
Stand/Clamps: For holding grating and laser securely
4
Theory
When monochromatic light passes through a diffraction grating, it produces a characteristic diffraction pattern due to the interference of light waves from multiple parallel slits or rulings.
A diffraction grating consists of a large number of equally spaced parallel slits. When coherent light (like laser light) is incident on the grating, each slit acts as a source of secondary wavelets according to Huygens' principle. These wavelets interfere constructively and destructively to produce bright and dark fringes on a screen.
Constructive Interference: Occurs when the path difference between light from adjacent slits equals an integer multiple of the wavelength, resulting in bright maxima.
Destructive Interference: Occurs when the path difference equals an odd multiple of half wavelengths, resulting in dark minima.
The grating equation relates the wavelength of light to the grating spacing and the angle of diffraction. This experiment allows us to determine the unknown wavelength of laser light by measuring the positions of diffraction maxima.
6
Procedure
1
Set up the laser source on an optical bench and ensure it produces a stable, coherent beam.
2
Mount the diffraction grating perpendicular to the laser beam at a suitable distance from the source.
3
Place a white screen at a distance D (approximately 1-2 meters) from the grating to observe the diffraction pattern.
4
Switch on the laser and observe the diffraction pattern on the screen. You should see a bright central maximum and several orders of maxima on both sides.
5
Measure the distance D between the grating and the screen using a measuring scale.
6
Mark the positions of the central maximum (m=0) and the first few orders (m=1, 2, 3) on both sides of the central maximum.
7
Measure the distance x of each order from the central maximum and record the observations.
8
Repeat the measurements for different values of D to improve accuracy.
9
Note the grating specification (number of lines per mm or lines per inch) to calculate the grating spacing d.
7
Observation Table
Grating Specification: _______ lines/mm
Grating Spacing (d): _______ m
Distance between grating and screen (D): _______ m
| S. No. |
Order of Diffraction (m) |
Position of Left Maximum (cm) |
Position of Right Maximum (cm) |
Distance from Center x (cm) |
Average x (cm) |
Wavelength λ (nm) |
| 1 |
1 |
|
|
|
|
|
| 2 |
2 |
|
|
|
|
|
| 3 |
3 |
|
|
|
|
|
| 4 |
4 |
|
|
|
|
|
9
Result
The wavelength of the laser light = _______ nm
Theoretical/Expected wavelength = _______ nm
Percentage error = _______%
The experimental value of wavelength is in close agreement with the theoretical value, confirming the wave nature of light and validating the grating equation.
10
Precautions
⚠️ Laser Safety: Never look directly into the laser beam or its reflections. Always wear appropriate safety goggles when required.
📏 Measurement Accuracy: Ensure accurate measurement of distances using appropriate measuring instruments.
🔧 Alignment: Keep the grating perpendicular to the incident laser beam for proper diffraction pattern.
🎯 Screen Position: Maintain the screen parallel to the grating surface for accurate measurements.
💡 Room Lighting: Perform the experiment in a darkened room for better visibility of diffraction maxima.
📐 Multiple Readings: Take readings for multiple orders and calculate average wavelength to minimize errors.
🔍 Grating Care: Handle the diffraction grating carefully to avoid scratches or fingerprints on the surface.
📊 Recording: Record all observations carefully and double-check calculations for accuracy.
11
Viva Voice Questions
Q1. What is a diffraction grating and how does it work?
A diffraction grating is an optical component with a regular pattern of slits or lines that diffracts light into its component wavelengths. It works on the principle of interference of light waves from multiple sources, creating constructive and destructive interference patterns.
Q2. State and explain the grating equation.
The grating equation is d sin θ = mλ, where d is the grating spacing, θ is the diffraction angle, m is the order of diffraction, and λ is the wavelength. This equation describes the condition for constructive interference at the maxima.
Q3. What is the difference between diffraction and interference?
Diffraction is the bending of waves around obstacles or through apertures, while interference is the superposition of two or more waves. Diffraction grating combines both phenomena - diffraction at each slit and interference between waves from different slits.
Q4. Why do we use laser light instead of ordinary light?
Laser light is coherent (constant phase relationship), monochromatic (single wavelength), and highly directional, making it ideal for producing sharp, well-defined diffraction patterns. Ordinary light lacks these properties and would produce blurred patterns.
Q5. What happens to the diffraction pattern if we increase the number of lines per unit length of the grating?
Increasing the number of lines per unit length (decreasing grating spacing d) increases the separation between diffraction orders, making the pattern more spread out. The maxima become sharper and more intense.
Q6. What is the significance of different orders of diffraction?
Different orders (m = 0, ±1, ±2, ...) represent different angles at which constructive interference occurs. Higher orders are farther from the center and generally less intense. The zero order is the undiffracted beam.
Q7. How does the wavelength of light affect the diffraction pattern?
Longer wavelengths produce more widely spaced diffraction patterns, while shorter wavelengths produce more closely spaced patterns. This is why red light spreads more than blue light in a diffraction grating.
Q8. What are the sources of error in this experiment?
Sources of error include: inaccurate distance measurements, misalignment of apparatus, finite width of laser beam, approximation of small angles, parallax errors in reading positions, and imperfections in the grating.
Q9. What is the resolving power of a diffraction grating?
Resolving power is the ability to distinguish between two close wavelengths. For a grating, it equals mN, where m is the order and N is the total number of lines illuminated. Higher resolving power means better spectral resolution.
Q10. Applications of diffraction gratings in real life?
Diffraction gratings are used in spectrometers for wavelength analysis, optical encoders for position measurement, laser wavelength selection, CD/DVD data storage and reading, and in various optical instruments for spectroscopy.