Lab Manual - Resolving Power of Telescope

To Determine the Resolving Power of Telescope

1 Aim

To determine the Resolving Power of a given telescope using Rayleigh's criterion and to verify the theoretical relationship between resolving power, wavelength of light, and aperture of the telescope.

2 Apparatus Used

Telescope
(Astronomical telescope with known aperture)

Double Slit
(With known slit separation)

Sodium Lamp
(Monochromatic source, λ = 589.3 nm)

Screen
(For observing interference pattern)

Meter Scale
(For distance measurements)

Vernier Calipers
(For measuring small dimensions)

3 Diagram

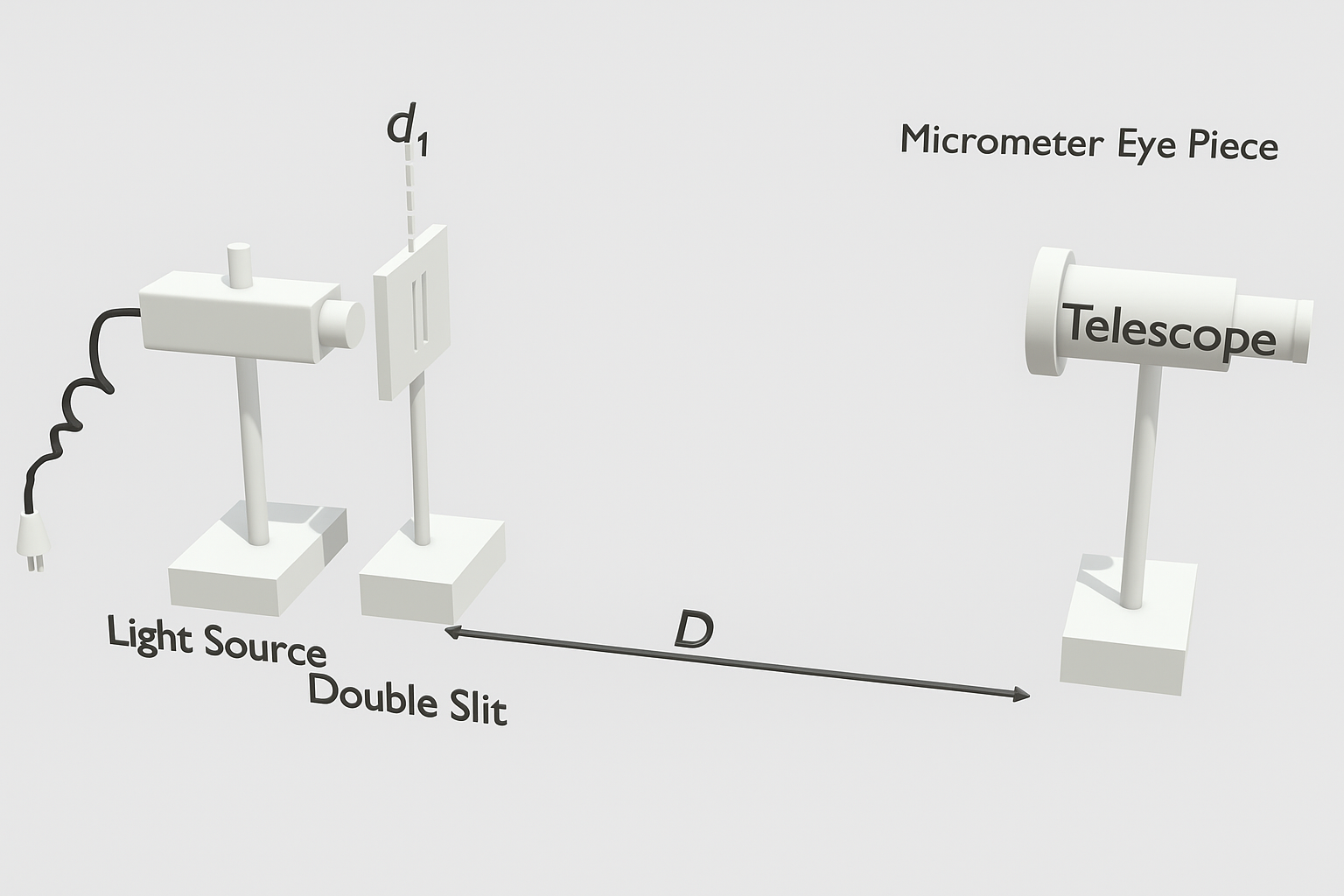
Experimental Setup

4 Theory

MathJax failed to load. Mathematical expressions may not display correctly.

The resolving power of an optical instrument is its ability to distinguish between two closely spaced objects. For a telescope, this is governed by the diffraction of light at the objective lens or mirror.

According to Rayleigh's criterion, two point sources are just resolved when the central maximum of the diffraction pattern of one source coincides with the first minimum of the diffraction pattern of the other source.

For a circular aperture (telescope objective), the angular resolution is given by the Rayleigh criterion. The resolving power is defined as the reciprocal of the minimum angular separation that can be resolved.

When observing two closely spaced slits through a telescope, the slits will appear just resolved when their angular separation equals the theoretical limit of resolution of the telescope.

5 Formula

Angular Resolution (Rayleigh Criterion)

$$\theta = 1.22 \frac{\lambda}{D}$$

Resolving Power

$$R.P. = \frac{1}{\theta} = \frac{D}{1.22\lambda}$$

Angular Separation of Slits

$$\theta = \frac{d}{L}$$

Condition for Just Resolution

$$\frac{d}{L} = 1.22 \frac{\lambda}{D}$$

Where:

θ = Angular resolution (radians)

λ = Wavelength of light (m)

D = Diameter of telescope aperture (m)

d = Slit separation (m)

L = Distance between slits and telescope (m)

R.P. = Resolving Power

6 Procedure

1 Set up the sodium lamp and allow it to warm up for proper illumination.

2 Place the double slit at a suitable distance from the sodium lamp to get uniform illumination.

3 Position the telescope at a large distance (at least 2-3 meters) from the double slit.

4 Measure the aperture diameter (D) of the telescope objective using vernier calipers.

5 Look through the telescope and adjust the focus to see the double slit clearly.

6 Gradually reduce the aperture of the telescope using an iris diaphragm or cardboard with circular holes of different diameters.

7 For each aperture diameter, find the maximum distance L at which the two slits are just resolved.

8 Record the aperture diameter D and corresponding distance L for just resolution.

9 Repeat the experiment with different aperture diameters.

10 Measure the slit separation 'd' using vernier calipers.

7 Observation Table

Given:

Wavelength of sodium light (λ) = 589.3 × 10⁻⁹ m

Slit separation (d) = _____ mm = _____ × 10⁻³ m

S.No.	Aperture Diameter D (mm)	Distance for Just Resolution L (m)	Angular Resolution θ = d/L (rad)	Theoretical θ 1.22λ/D (rad)	Resolving Power R.P. = D/(1.22λ)	% Error
1
2
3
4
5

8 Calculations

Sample Calculation

Given:

D = _____ mm = _____ × 10⁻³ m

L = _____ m

d = _____ × 10⁻³ m

λ = 589.3 × 10⁻⁹ m

Experimental Angular Resolution

$$\theta_{exp} = \frac{d}{L} = \frac{\_\_\_\_\_}{\_\_\_\_\_} = \_\_\_\_\_ \text{ radians}$$

Theoretical Angular Resolution

$$\theta_{theo} = 1.22 \frac{\lambda}{D} = 1.22 \times \frac{589.3 \times 10^{-9}}{\_\_\_\_\_} = \_\_\_\_\_ \text{ radians}$$

Resolving Power

$$R.P. = \frac{D}{1.22\lambda} = \frac{\_\_\_\_\_}{1.22 \times 589.3 \times 10^{-9}} = \_\_\_\_\_$$

Percentage Error

$$\text{Error \%} = \frac{|\theta_{theo} - \theta_{exp}|}{\theta_{theo}} \times 100 = \_\_\_\_\_ \%$$

9 Result

1. The resolving power of the given telescope is found to be ____________.

2. The experimental values of angular resolution are in good agreement with the theoretical values predicted by Rayleigh's criterion.

3. The resolving power is found to be directly proportional to the aperture diameter and inversely proportional to the wavelength of light used.

4. The average percentage error in the experiment is ______%.

10 Precautions

1 Ensure the sodium lamp is properly warmed up before taking observations.

2 Keep the telescope at a sufficiently large distance from the double slit to avoid parallax errors.

3 Adjust the telescope focus carefully to get sharp images of the slits.

4 Take multiple readings and calculate the average to minimize random errors.

5 Ensure proper alignment of the optical components to avoid systematic errors.

6 Measure the aperture diameter and slit separation accurately using vernier calipers.

7 Avoid vibrations during the experiment as they can affect the resolution observations.

8 Work in a dimly lit room to better observe the resolution limit.

11 Viva Voice Questions

Q1: What is meant by resolving power of a telescope?

Q2: State Rayleigh's criterion for resolution.

Q3: How does the resolving power depend on the aperture of the telescope?

Q4: What is the difference between magnifying power and resolving power?

Q5: Why is monochromatic light used in this experiment?

Q6: What happens to the resolving power if we use blue light instead of sodium light?

Q7: Explain the physical significance of the factor 1.22 in the resolution formula.

Q8: Why do larger telescopes have better resolving power?

Q9: What is the difference between resolution and magnification?

Q10: How does atmospheric turbulence affect the resolving power of ground-based telescopes?

For More experiment Manual Click on Link...