Determination of Magnetic Susceptibility by Guoy's Balance Method
1. Aim
To determine the magnetic susceptibility of a paramagnetic or diamagnetic sample using Guoy's balance method.
2. Apparatus Used
- Guoy's balance with sample tube
- Electromagnet with power supply
- Ammeter (0-5A)
- Rheostat
- Magnetic sample (paramagnetic/diamagnetic material)
- Analytical balance (sensitivity 0.001g)
- Vernier caliper
- Connecting wires
- Weighing tube
- Gauss meter (optional, for field measurement)
3. Diagram
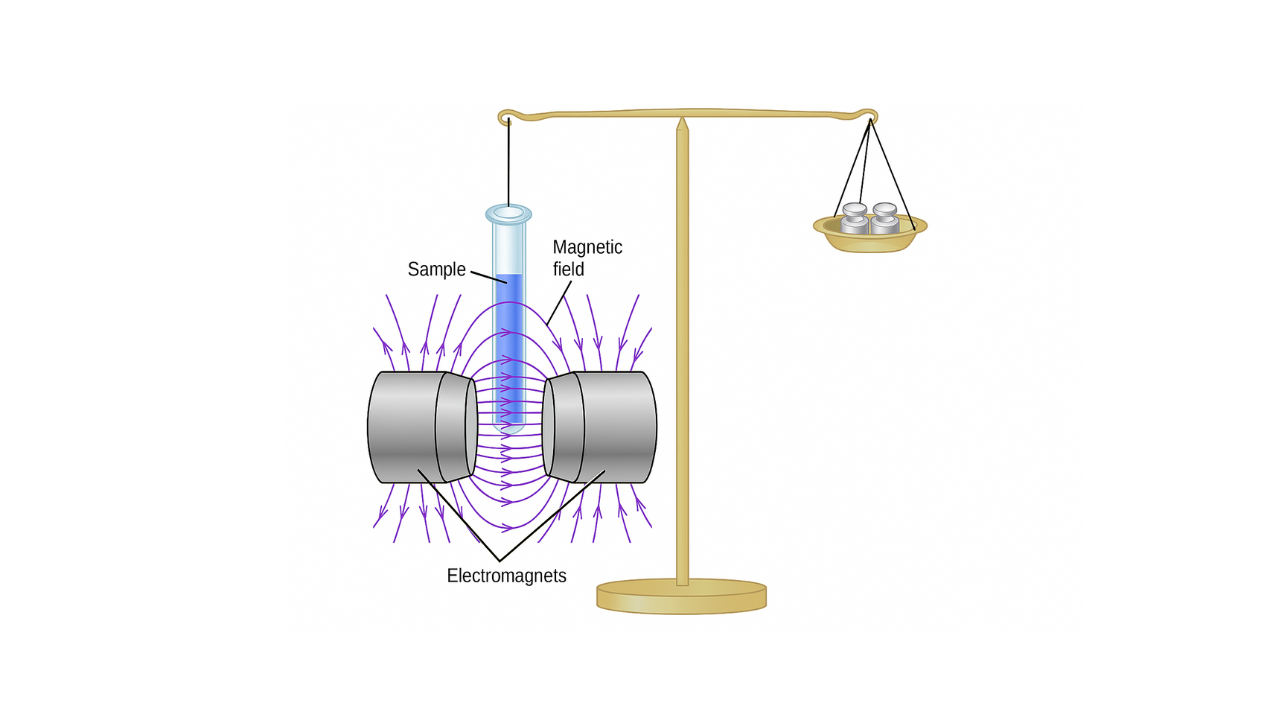
Figure 1: Experimental setup for Guoy's Balance method
4. Theory
Guoy's balance method is a technique used to measure the magnetic susceptibility of materials, particularly those with weak magnetic properties (paramagnetic and diamagnetic substances).
When a material is placed in a non-uniform magnetic field, it experiences a force that depends on its magnetic susceptibility. For a paramagnetic substance, the force is directed toward the stronger part of the field, while for a diamagnetic substance, it is directed away from the stronger part of the field.
The magnetic susceptibility (χ) is a dimensionless quantity that measures the degree of magnetization of a material in response to an applied magnetic field. Mathematically, it is defined as:
$\chi = \frac{M}{H}$
Where:
- M is the magnetization induced in the material (magnetic moment per unit volume)
- H is the applied magnetic field intensity
In Guoy's method, a cylindrical sample is suspended from one arm of a sensitive balance such that one end of the sample is in a region of strong magnetic field while the other end is in a region of negligible field. The apparent change in weight of the sample when the magnetic field is applied is measured and used to calculate the magnetic susceptibility.
For a paramagnetic substance, there's an apparent increase in weight when the field is turned on, while for a diamagnetic substance, there's an apparent decrease in weight.
When the sample is placed in a non-uniform magnetic field, the force experienced by it is given by:
$F = \frac{1}{2}\chi V \mu_0 \nabla(H^2)$
Where:
- F is the force on the sample
- χ is the magnetic susceptibility
- V is the volume of the sample
- μ₀ is the permeability of free space (4π × 10⁻⁷ H/m)
- ∇(H²) is the gradient of the square of the magnetic field intensity
In the Guoy's balance setup, this force is measured as an apparent change in weight, and the susceptibility is calculated accordingly.
5. Formula
The volume magnetic susceptibility (χ) of the sample can be calculated using the formula:
$\chi = \frac{2g\Delta m}{AH^2\mu_0}$
Where:
- Δm is the change in mass (apparent change in weight when the field is turned on)
- g is the acceleration due to gravity (9.8 m/s²)
- A is the cross-sectional area of the sample
- H is the magnetic field intensity
- μ₀ is the permeability of free space (4π × 10⁻⁷ H/m)
Alternatively, the mass susceptibility (χₘ) can be calculated as:
$\chi_m = \frac{\chi}{\rho}$
Where ρ is the density of the sample.
For practical purposes, when the field gradient is not known directly, a calibration with a substance of known susceptibility can be used:
$\chi = \chi_{std} \cdot \frac{\Delta m \cdot \rho_{std}}{\Delta m_{std} \cdot \rho}$
Where the subscript 'std' refers to the standard substance with known susceptibility.
6. Procedure
- Set up the Guoy's balance with the electromagnet as shown in the diagram. Ensure that the sample tube is properly aligned with the balance.
- Measure the cross-sectional area of the sample tube using a vernier caliper.
- Weigh the empty sample tube accurately using the analytical balance.
- Fill the sample tube with the magnetic material under investigation. Ensure that the material is packed uniformly without air gaps.
- Weigh the filled sample tube to determine the mass of the sample.
- Suspend the sample tube from one arm of the balance such that its lower end is positioned between the poles of the electromagnet (in the region of maximum field gradient).
- Note the initial reading of the balance with the magnetic field turned off.
- Turn on the electromagnet and gradually increase the current using the rheostat. Record the balance reading and corresponding current values.
- Increase the current in steps (e.g., 0.5A intervals) up to the maximum allowable limit, noting the balance reading at each step.
- Decrease the current in the same steps, recording the balance readings again to check for hysteresis effects.
- Turn off the magnetic field and verify that the balance returns to its initial reading.
- If available, use a Gauss meter to measure the magnetic field at different current values.
- Repeat the experiment 2-3 times for consistency.
- Calculate the magnetic susceptibility using the appropriate formula.
7. Observation Table
| Sample Details | ||||||
|---|---|---|---|---|---|---|
| Material Name: ____________ | Cross-sectional Area (A): ________ m² | |||||
| Mass of Empty Tube: ________ g | Mass of Tube with Sample: ________ g | |||||
| Mass of Sample (m): ________ g | Density of Sample (ρ): ________ kg/m³ | |||||
| Measurements | ||||||
| S.No. | Current (A) | Field Strength, H (A/m) | Balance Reading (g) | Change in Weight, Δm (g) | Susceptibility, χ | |
| Field OFF | Field ON | |||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
Note: The field strength H can be determined from the current using calibration data or measured directly with a Gauss meter.
8. Calculations
Step 1: Calculate the change in weight (Δm) for each current value:
$\Delta m = \text{Balance reading (Field ON)} - \text{Balance reading (Field OFF)}$
Step 2: Determine the magnetic field intensity (H) at the sample position for each current value. This can be done using calibration data or direct measurement with a Gauss meter.
Step 3: Calculate the volume magnetic susceptibility (χ) using the formula:
$\chi = \frac{2g\Delta m}{AH^2\mu_0}$
Step 4: Calculate the mass susceptibility (χₘ):
$\chi_m = \frac{\chi}{\rho}$
Step 5: Calculate the molar susceptibility (χₘₒₗ), if required:
$\chi_{mol} = \chi_m \times \text{Molar mass}$
Step 6: Plot a graph of Δm versus H² to verify the linear relationship and to obtain a more accurate value of susceptibility from the slope.
Sample Calculation:
Let's assume the following values:
- Change in weight (Δm) = 0.002 g
- Cross-sectional area of sample (A) = 5 × 10⁻⁵ m²
- Magnetic field (H) = 5 × 10⁵ A/m
- Permeability of free space (μ₀) = 4π × 10⁻⁷ H/m
- Acceleration due to gravity (g) = 9.8 m/s²
Substituting in the formula:
$\chi = \frac{2 \times 9.8 \times 0.002}{5 \times 10^{-5} \times (5 \times 10^5)^2 \times 4\pi \times 10^{-7}}$
$\chi = \frac{0.0392}{4\pi \times 10^{-7} \times 5 \times 10^{-5} \times 25 \times 10^{10}}$
$\chi = \frac{0.0392}{4\pi \times 5 \times 25 \times 10^{-2}}$
$\chi = \frac{0.0392}{4\pi \times 5 \times 25 \times 10^{-2}} = \frac{0.0392}{1.57 \times 125 \times 10^{-2}} = \frac{0.0392}{1.9625} = 0.020 \text{ (dimensionless)}$
If the density of the sample is 2500 kg/m³, then the mass susceptibility is:
$\chi_m = \frac{0.020}{2500} = 8 \times 10^{-6} \text{ m³/kg}$
9. Result
The volume magnetic susceptibility (χ) of the given sample is ____________ (dimensionless).
The mass magnetic susceptibility (χₘ) of the given sample is ____________ m³/kg.
Based on the sign and magnitude of the susceptibility, the sample is classified as:
- If χ > 0: Paramagnetic material
- If χ < 0: Diamagnetic material
- If χ >> 0: Ferromagnetic or ferrimagnetic material
Comments: [Include any observations regarding the behavior of the sample, sources of error, etc.]
10. Precautions
- Ensure that the Guoy's balance is properly calibrated and leveled before starting the experiment.
- The sample tube should be properly aligned with respect to the magnetic field to ensure that it experiences the maximum field gradient.
- The sample should be packed uniformly in the tube without air gaps to avoid errors in measurement.
- Handle the sample tube carefully to avoid spilling the material or changing its position during the experiment.
- Allow sufficient time for the balance to stabilize before taking readings.
- Ensure that there are no magnetic materials or electronic devices near the balance that could interfere with the measurements.
- Maintain a constant temperature during the experiment, as magnetic susceptibility can vary with temperature.
- Avoid excessive currents that may cause heating of the electromagnet coils, affecting the field strength.
- Take multiple readings for each current value and use the average for calculations to minimize random errors.
- For highly magnetic samples, use smaller amounts to avoid saturation effects.
- Check for hysteresis effects by increasing and decreasing the field and noting any differences in readings.
- Ensure that the balance is protected from air currents during measurements.
11. Viva Voice Questions
Q1: What is magnetic susceptibility? How is it related to permeability?
A1: Magnetic susceptibility (χ) is a dimensionless quantity that measures how much a material will become magnetized in an applied magnetic field. It is related to relative permeability (μᵣ) by the equation: μᵣ = 1 + χ, where μᵣ is the ratio of the permeability of the material to the permeability of free space.
Q2: Differentiate between diamagnetic, paramagnetic, and ferromagnetic materials.
A2:
- Diamagnetic materials: Have negative susceptibility (χ < 0). They are weakly repelled by magnetic fields. Examples include copper, gold, and bismuth.
- Paramagnetic materials: Have small positive susceptibility (χ > 0). They are weakly attracted by magnetic fields. Examples include aluminum, platinum, and oxygen.
- Ferromagnetic materials: Have very large positive susceptibility (χ >> 0). They are strongly attracted by magnetic fields and can retain magnetization. Examples include iron, nickel, and cobalt.
Q3: Why is Guoy's method suitable for measuring weak magnetic properties?
A3: Guoy's method is suitable for measuring weak magnetic properties because it directly measures the force experienced by the material in a non-uniform magnetic field, which is proportional to its susceptibility. The method uses a sensitive balance to detect small changes in weight, making it ideal for materials with low susceptibility like paramagnetic and diamagnetic substances.
Q4: What are the limitations of Guoy's balance method?
A4: Limitations include:
- Requirement for a large amount of sample material
- Sensitivity to environmental disturbances like air currents and vibrations
- Difficulty in maintaining uniform packing density of powdered samples
- Limited accuracy for materials with very low susceptibility
- Need for precise calibration of the magnetic field gradient
- Assumes that the sample behaves linearly with field strength
Q5: How does temperature affect magnetic susceptibility?
A5: Temperature affects magnetic susceptibility differently for different types of materials:
- For diamagnetic materials, susceptibility is generally independent of temperature.
- For paramagnetic materials, susceptibility varies inversely with absolute temperature (Curie's law): χ ∝ 1/T.
- For ferromagnetic materials, susceptibility decreases with increasing temperature and drops dramatically at the Curie temperature, above which they become paramagnetic.
Q6: What is the significance of the sign of magnetic susceptibility?
A6: The sign of magnetic susceptibility indicates the type of magnetic behavior:
- Negative susceptibility (χ < 0) indicates diamagnetic behavior, where the induced magnetization opposes the applied field.
- Positive susceptibility (χ > 0) indicates paramagnetic or ferromagnetic behavior, where the induced magnetization aligns with the applied field.
Q7: Why do we need a non-uniform magnetic field in Guoy's method?
A7: A non-uniform magnetic field (field gradient) is essential in Guoy's method because it creates a net force on the sample. In a uniform field, a magnetic material would experience equal and opposite forces at its ends, resulting in no net force. The field gradient creates an imbalance in these forces, leading to a measurable force proportional to the magnetic susceptibility.
Q8: Name some alternative methods for measuring magnetic susceptibility.
A8: Alternative methods include:
- Faraday's method (using a magnetic balance)
- SQUID magnetometry (Superconducting Quantum Interference Device)
- Vibrating Sample Magnetometer (VSM)
- AC susceptibility measurements
- Evans method (NMR-based technique)
- Force methods using electromagnets with shaped pole pieces
Q9: What is the relationship between magnetization, magnetic field strength, and susceptibility?
A9: The relationship is given by the equation: M = χH, where M is the magnetization (magnetic moment per unit volume), χ is the magnetic susceptibility, and H is the magnetic field strength. This linear relationship holds for diamagnetic and paramagnetic materials at moderate field strengths, but not for ferromagnetic materials which show non-linear behavior.
Q10: How would you verify that your experimental setup is working correctly?
A10: To verify the experimental setup:
- Measure a standard reference material with known susceptibility (e.g., water or copper sulfate)
- Check for linear relationship between change in weight and square of field strength
- Verify that the balance returns to zero when field is turned off
- Ensure repeatability of measurements
- Check that paramagnetic samples show weight increase and diamagnetic samples show weight decrease
