To determine coefficient of restitution for inelastic collision
Loading mathematical equations...
1. AIM
To determine the coefficient of restitution between different objects during inelastic collision by measuring the height of release and rebound.
2. APPARATUS USED
- Two spherical balls of different materials (e.g., rubber ball, tennis ball, steel ball, etc.)
- A smooth, hard, and flat surface (e.g., marble/granite slab or floor)
- Meter scale/measuring tape
- Clamp stand with clamp
- Graph paper
- Calculator
- Stopwatch (optional for alternative method)
- Plumb line and spirit level (to ensure surface is horizontal)
3. DIAGRAM
Figure : Experimental setup showing a ball dropped from height h₁ rebounding to height h₂ after collision
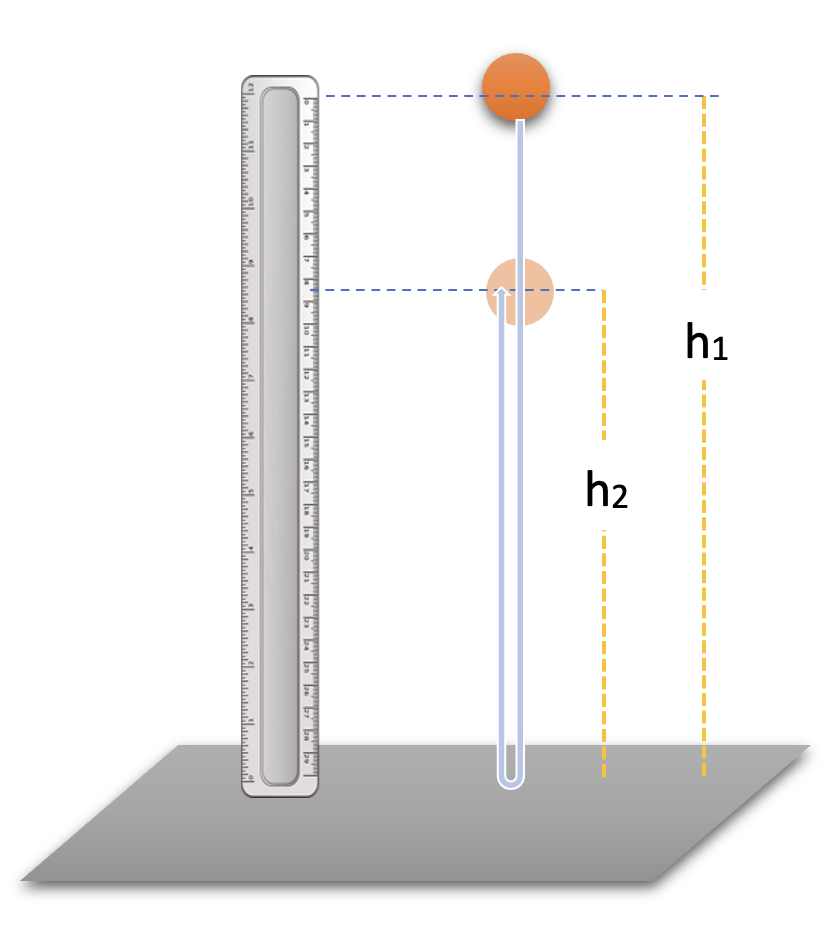
4. THEORY
When a ball is dropped from a certain height onto a surface, it undergoes an inelastic collision with the surface. The collision is characterized by some loss of kinetic energy, which means the ball won't rebound to its original height.
The coefficient of restitution (e) is a measure of the elasticity of the collision between two objects. It is defined as the ratio of the relative velocity of separation after collision to the relative velocity of approach before collision.
For a ball dropped onto a horizontal surface:
- If e = 1, the collision is perfectly elastic (no energy loss)
- If 0 < e < 1, the collision is inelastic (some energy loss)
- If e = 0, the collision is perfectly inelastic (maximum energy loss, no rebound)
When a ball is dropped from height h₁ and rebounds to height h₂, we can derive the coefficient of restitution using energy conservation principles.
5. FORMULA
When a ball falls from height h₁, its velocity just before impact is:
\[ v_1 = \sqrt{2gh_1} \]
After collision, its initial rebound velocity is:
\[ v_2 = \sqrt{2gh_2} \]
The coefficient of restitution is:
\[ e = \frac{v_2}{v_1} = \frac{\sqrt{2gh_2}}{\sqrt{2gh_1}} = \sqrt{\frac{h_2}{h_1}} \]
Therefore:
\[ e = \sqrt{\frac{h_2}{h_1}} \]
Where:
- e = coefficient of restitution
- h₁ = height from which the ball is dropped
- h₂ = height to which the ball rebounds
- g = acceleration due to gravity
6. PROCEDURE
- Place the flat surface horizontally. Use a spirit level to ensure it is perfectly horizontal.
- Set up the meter scale vertically next to the surface using the clamp stand.
- Take one of the balls and hold it at a measured height h₁ (e.g., 100 cm) above the horizontal surface.
- Release the ball (without giving it any push) and carefully observe the maximum height h₂ to which it rebounds.
- Repeat this process at least 5 times for the same height to get an average value.
- Repeat steps 3-5 for different heights of release (e.g., 80 cm, 60 cm, etc.).
- Repeat the entire experiment with another ball of different material.
- Record all observations in the observation table.
- Calculate the coefficient of restitution for each trial using the formula e = √(h₂/h₁).
- Calculate the average coefficient of restitution for each ball.
7. OBSERVATION TABLE
Table 1: Determination of Coefficient of Restitution for Ball 1 (Material: _______)
| Trial No. | Height of release, h₁ (cm) | Height of rebound, h₂ (cm) | Coefficient of restitution, e = √(h₂/h₁) |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| Average |
Table 2: Determination of Coefficient of Restitution for Ball 2 (Material: _______)
| Trial No. | Height of release, h₁ (cm) | Height of rebound, h₂ (cm) | Coefficient of restitution, e = √(h₂/h₁) |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| Average |
8. CALCULATIONS
Sample calculation for one trial:
Given:
- Height of release (h₁) = 100 cm
- Height of rebound (h₂) = 64 cm
Coefficient of restitution (e) = √(h₂/h₁)
\[ e = \sqrt{\frac{64}{100}} \]
\[ e = \sqrt{0.64} \]
\[ e = 0.8 \]
The average coefficient of restitution for each ball is calculated by taking the mean of all trial values.
9. RESULT
- The coefficient of restitution for Ball 1 (Material: _______) = _______ ± _______ (with uncertainty/error)
- The coefficient of restitution for Ball 2 (Material: _______) = _______ ± _______ (with uncertainty/error)
10. PRECAUTIONS
- Ensure the horizontal surface is completely flat and rigid.
- Release the ball without giving it any initial velocity (no pushing).
- Take readings from eye level to avoid parallax error.
- The ball should fall vertically without any spin or horizontal motion.
- Ensure there are no air currents that might affect the ball's motion.
- For accurate readings, the rebound height should be measured to the bottom of the ball.
- The surface should be clean and free from dust or impurities.
- Repeat each measurement multiple times to reduce random errors.
- Use balls that are perfectly spherical and uniform.
- Avoid surface dents or deformations that might affect the collision.
11. VIVA VOCE QUESTIONS
Q: What is the coefficient of restitution?
A: The coefficient of restitution is a measure of the elasticity of a collision between two objects. It is defined as the ratio of the relative velocity of separation after collision to the relative velocity of approach before collision.
Q: What does a coefficient of restitution value of 0 indicate?
A: A coefficient of restitution of 0 indicates a perfectly inelastic collision where the objects stick together after collision with maximum energy loss and no rebound.
Q: What does a coefficient of restitution value of 1 indicate?
A: A coefficient of restitution of 1 indicates a perfectly elastic collision where there is no loss of kinetic energy.
Q: Why is the coefficient of restitution always less than 1 in practical situations?
A: In practical situations, some energy is always converted to heat, sound, and material deformation during collisions, leading to energy loss and a coefficient less than 1.
Q: How does the height of release affect the coefficient of restitution?
A: Theoretically, the coefficient of restitution should be independent of the height of release. However, in practice, it might slightly decrease with increasing height due to deformation effects and air resistance.
Q: Why do different materials have different coefficients of restitution?
A: Different materials have different elastic properties, internal structures, and energy absorption capabilities, which affect how they deform and recover during collisions.
Q: How would temperature affect the coefficient of restitution?
A: Temperature can affect material properties. Generally, increased temperature decreases the elasticity of materials like rubber, resulting in a lower coefficient of restitution.
Q: What are some real-world applications of the coefficient of restitution?
A: It's used in sports equipment design (balls, rackets), automotive safety (crash analysis), industrial processes (material handling), and computer simulations of collisions.
Q: How would the coefficient of restitution change if the experiment were conducted on the moon?
A: The coefficient of restitution is independent of gravity, so it would remain the same on the moon. However, the ball would fall more slowly and rebound slower due to lower gravity.
Q: Can the coefficient of restitution be greater than 1? Why or why not?
A: Theoretically, the coefficient of restitution cannot exceed 1 as this would violate the law of conservation of energy, suggesting more energy after collision than before, which is impossible in an isolated system.