There was an error loading the mathematical equations. Please refresh the page or check your internet connection.
Surface Tension Determination by Jaeger's Method
1. Aim
To determine the surface tension of a given liquid using Jaeger's method by measuring the maximum pressure required to form bubbles at the end of a capillary tube.
2. Apparatus Used
- Jaeger's apparatus (consisting of a pressure manometer and a capillary tube)
- Traveling microscope
- Mercury manometer or pressure sensor
- Thermometer
- Beaker
- Test liquid (water, alcohol, etc.)
- Screw gauge
- Magnifying glass
- Stopwatch
- Rubber tubing and connector
- Retort stand with clamps
- Spirit level
3. Diagram
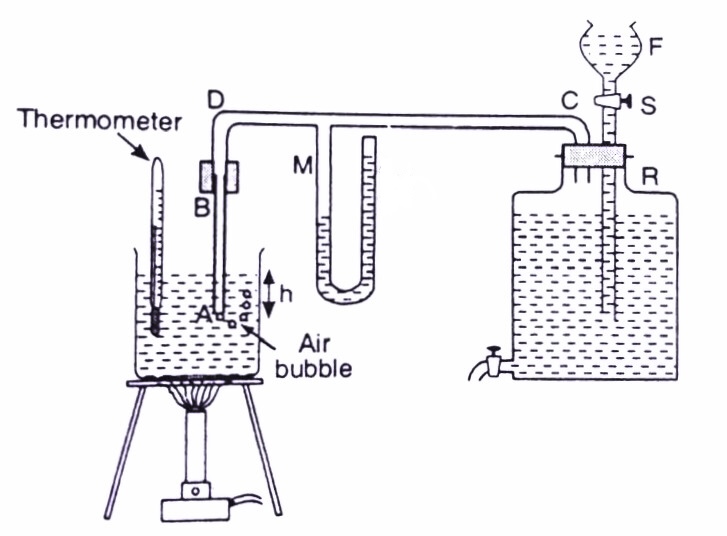
Fig: Schematic diagram of Jaeger's apparatus for measuring surface tension
4. Theory
The Jaeger's method for measuring surface tension is based on the principle that when air is forced through a capillary tube immersed in a liquid, the maximum pressure required to form a bubble is related to the surface tension of the liquid.
When the tip of a capillary tube is immersed in a liquid, the pressure required to form a bubble at the end of the tube depends on:
- The surface tension of the liquid
- The radius of the capillary tube
- The depth of immersion of the capillary tip
According to Jaeger's method, the maximum pressure (P) required to form a bubble at the end of a capillary tube of radius 'r' immersed to a depth 'h' in a liquid of density 'ρ' is given by:
\[P = P_0 + \rho gh + \frac{2T}{r}\]
Where:
- \(P_0\) is the atmospheric pressure
- \(\rho\) is the density of the liquid
- \(g\) is the acceleration due to gravity
- \(h\) is the depth of immersion
- \(T\) is the surface tension of the liquid
- \(r\) is the radius of the capillary tube
For two different depths of immersion \(h_1\) and \(h_2\), the difference in maximum pressures will be:
\[P_2 - P_1 = \rho g(h_2 - h_1)\]
By measuring the maximum pressure at different depths, we can determine the surface tension of the liquid.
5. Formula
The surface tension (T) of the liquid is given by:
\[T = \frac{(P - \rho gh)r}{2}\]
Where:
- \(P\) is the maximum pressure required to form a bubble
- \(\rho\) is the density of the liquid
- \(g\) is the acceleration due to gravity
- \(h\) is the depth of immersion
- \(r\) is the radius of the capillary tube
Alternatively, using Jaeger's simplified method with two different depths (\(h_1\) and \(h_2\)):
\[T = \frac{[P_2 - P_1 - \rho g(h_2 - h_1)]r}{2}\]
Where \(P_1\) and \(P_2\) are the maximum pressures at depths \(h_1\) and \(h_2\) respectively.
6. Procedure
Setup Preparation:
- Clean the apparatus thoroughly to remove any impurities.
- Fill the beaker with the test liquid.
- Mount the capillary tube vertically using a retort stand and clamp.
- Connect the capillary tube to the manometer using rubber tubing.
Measurement of Capillary Radius:
- Use a screw gauge to measure the diameter of the capillary tube at different positions.
- Take at least 5 readings and calculate the average radius.
Measurement of Surface Tension:
- Immerse the capillary tube in the liquid to a small depth (\(h_1\)).
- Measure this depth accurately using a traveling microscope.
- Gradually increase the pressure in the system until bubbles just begin to form at the tip of the capillary.
- Record the maximum pressure (\(P_1\)) indicated by the manometer at which bubbles are formed.
- Repeat the measurement 5 times and take the average value of \(P_1\).
Repeat for Different Depths:
- Change the depth of immersion to a new value (\(h_2\)).
- Measure this new depth accurately.
- Determine the maximum pressure (\(P_2\)) required for bubble formation at this depth.
- Repeat 5 times and calculate the average value of \(P_2\).
Temperature Measurement:
- Record the temperature of the liquid using the thermometer.
Calculations:
- Substitute the measured values in the formula to calculate the surface tension of the liquid.
7. Observation Table
Table 1: Measurement of Capillary Radius
| Reading No. | Screw Gauge Reading (mm) | Radius (r) = Diameter/2 (mm) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| Average |
Table 2: Measurement of Pressure at Different Depths
| Reading No. | Depth h₁ (cm) | Maximum Pressure P₁ (N/m²) | Depth h₂ (cm) | Maximum Pressure P₂ (N/m²) |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| Average |
Additional Information:
- Temperature of liquid: ______ °C
- Density of liquid at experimental temperature: ______ kg/m³
- Acceleration due to gravity (g): 9.8 m/s²
- Temperature of liquid: ______ °C
- Density of liquid at experimental temperature: ______ kg/m³
- Acceleration due to gravity (g): 9.8 m/s²
8. Calculations
-
Calculate the average radius of the capillary tube:
\[ r = \frac{r_1 + r_2 + r_3 + r_4 + r_5}{5} \] -
Calculate the average maximum pressures at depths \(h_1\) and \(h_2\):
\[ P_1(avg) = \frac{P_{11} + P_{12} + P_{13} + P_{14} + P_{15}}{5} \] \[ P_2(avg) = \frac{P_{21} + P_{22} + P_{23} + P_{24} + P_{25}}{5} \] -
Calculate the surface tension using the formula:
\[ T = \frac{[P_2(avg) - P_1(avg) - \rho g(h_2 - h_1)]r}{2} \]
Sample Calculation:
Given:
- r = 0.5 mm = 0.0005 m
- h₁ = 2 cm = 0.02 m
- h₂ = 4 cm = 0.04 m
- P₁(avg) = 2000 N/m²
- P₂(avg) = 2400 N/m²
- ρ = 1000 kg/m³ (for water)
- g = 9.8 m/s²
Calculation:
\begin{align*}
T &= \frac{[2400 - 2000 - 1000 \times 9.8 \times (0.04 - 0.02)] \times 0.0005}{2} \\
&= \frac{[400 - 196] \times 0.00025}{1} \\
&= \frac{204 \times 0.00025}{1} \\
&= 0.051 \, \text{N/m}
\end{align*}
9. Result
The surface tension of the given liquid at ______ °C is ______ N/m.
(Compare this with the standard value of the liquid at the same temperature, if available, and calculate the percentage error.)
\[ \text{Percentage Error} = \left| \frac{\text{Experimental Value} - \text{Standard Value}}{\text{Standard Value}} \right| \times 100\% \]
10. Precautions
Ensure that the capillary tube is clean and free from grease or contaminants.
The capillary tube should be held perfectly vertical during the experiment.
Measure the radius of the capillary tube accurately, as small errors can significantly affect the result.
Control the pressure increase gradually to accurately determine the maximum pressure.
Ensure that the tip of the capillary tube is perfectly flat and perpendicular to its axis.
Record the temperature of the liquid as the surface tension is temperature-dependent.
The liquid level in the beaker should remain constant throughout the experiment.
Avoid any vibrations during pressure measurements.
Wait for the liquid to settle after each bubble forms before taking the next reading.
The capillary tube should be immersed to the exact measured depth.
Ensure there are no air leaks in the pressure system.
Take multiple readings at each depth to minimize random errors.
11. Viva Voce Questions
Q: What is surface tension and what causes it?
A: Surface tension is the property of a liquid's surface that makes it behave like an elastic sheet. It is caused by the cohesive forces between liquid molecules being stronger at the surface than the adhesive forces with the surrounding air molecules.
Q: How does temperature affect the surface tension of a liquid?
A: Generally, the surface tension of a liquid decreases with increasing temperature. This happens because higher temperatures increase the kinetic energy of molecules, reducing the effectiveness of cohesive forces.
Q: Why is the capillary tube immersed at different depths in Jaeger's method?
A: By measuring at different depths, we can eliminate the effect of atmospheric pressure and determine the pressure solely due to surface tension and hydrostatic pressure.
Q: What are some practical applications of surface tension?
A: Surface tension is important in capillary action, detergency, formation of drops and bubbles, floating of objects on liquid surfaces, mixing of liquids, and in biological systems like the functioning of lungs.
Q: Why must the capillary tube be thoroughly cleaned before the experiment?
A: Any contaminants or grease on the capillary tube can alter the surface tension measurements by changing the contact angle between the liquid and the tube.
Q: How does the radius of the capillary tube affect the pressure required for bubble formation?
A: The pressure required to form a bubble is inversely proportional to the radius of the capillary tube. A smaller radius requires higher pressure.
Q: What would happen to surface tension measurements if a surfactant is added to the liquid?
A: Surfactants lower the surface tension of liquids by disrupting the cohesive forces between molecules at the surface, resulting in lower measured values.
Q: How does Jaeger's method differ from other methods of measuring surface tension?
A: Jaeger's method measures the maximum pressure required to form bubbles, whereas other methods like the capillary rise method, drop weight method, or Du Noüy ring method use different physical principles.
Q: Why is it important to wait between bubble formations during measurements?
A: Waiting allows the liquid surface to settle and return to equilibrium, ensuring accurate pressure measurements for subsequent bubbles.
Q: How would you verify the accuracy of your surface tension measurement?
A: By comparing the experimental value with standard values for the same liquid at the same temperature, and by checking the reproducibility of results through multiple trials.